Planimetrie - slovní úlohy a příklady - strana 172 z 173
Počet nalezených příkladů: 3449
- Horizontální 83539
Elektrikář musí opravit elektrickou poruchu na sloupu o výšce 4 metry. Potřebuje dosáhnout bodu 1 m pod vrcholem. Jaká by měla být délka žebříku, který by mohl použít, když je nakloněný pod úhlem 60° od horizontální roviny? - Nedokončeného 83806
Úhel sklonu vrcholu nedokončeného pilíře v bodě 150 m od jeho základny je 30°. Má-li být úhel elevace ve stejném bodě 45°, pak se musí sloup zvednout do výšky o kolik metrů? - Pozorovací 83872
Muž stojící na palubě lodi, která je 10 m nad hladinou vody, pozoruje vrchol kopce při úhlu elevace 60° a pozorovací úhel sklonu paty kopce je 30°. Najděte vzdálenost kopce od lodi a výšku kopce. - Předpokladu 84214
Ve výšce 60 m nad zemí létá drak. Šňůrka připevněná k drakovi je dočasně přivázána k bodu na zemi. Sklon šňůry se zemí je 60°. Najděte délku šňůry za předpokladu, že šňůry je našponovaná a není volná.
- Věž + stožár
Na vodorovné rovině je svislá věž s vlajkovou tyčí na jejím vrcholu. V bodě vzdáleném 9 m od nohy věže je úhel elevace horní a dolní části vlajkové tyče 60° a 30°. Najděte výšku stožáru vlajky. - Pozorovací 84039
Dvaja muži sú na opačných stranách veže. Nameajú uhly elevácie (pozorovací) vrcholu veže jako 30° a druhý ako 45°. Ak je výška veže 50 m, nájdi vzdálenost medzi týmito dvoma mužmi. - Pozorovací 84353
Pozorovací úhel vrcholu věže od bodu A na zemi je 30°. Při přesunu na vzdálenost 20 m směrem k patě věže do bodu B se pozorovací úhel zvětší na 60°. Najděte výšku věže a vzdálenost věže od místa A . - Trojúhelník 83979
Podle nákresu - diagramu - najděte délky označené h a b. Jeden obdélník a jeden pravoúhlý trojúhelník sdílejí jednu stranu. Známe dva úhly a délku společné strany, jak je znázorněno na obrázku. - Souřadnice 83750
Souřadnice vrcholů ∆ABC jsou v tomto pořadí (-4, -2), (6, 2) a (4, 6). Najděte těžiště G ∆ABC .
- Trojúhelník - těžnice
Vrcholy trojúhelníku jsou A (-1,3), B (1,-1) a C (5, 1). Najděte délku těžnice z vrcholu C. - Pozorovací 84154
Z bodu A na zemi je pozorovací úhel vrcholu 20 m vysoké budovy 45°. Na vrcholu budovy je vztyčená vlajka a pozorovací úhel vrcholu vlajkové tyče od A je 60°. Najděte délku vlajkové tyče a vzdálenost budovy od bodu A. - Vzdálenost 81986
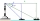Maják má výhled na záliv a je vysoký 77 metrů. Z vrchu může strážce majáku vidět jachtu na jih pod úhlem deprese 32 stupňů a další loď na východ pod úhlem 25 stupňů. Jaká je vzdálenost mezi čluny? - Trojúhelník 81517
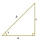Pravý trojúhelník má délky stran a=3, b=5 a c=4, jak je znázorněno níže. Použijte tyto délky k nalezení tan x, sin x a cos x. - Vzdálenost 84361
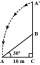Strom se vlivem bouře zlomí a zlomená část se ohne tak, že se vrchol stromu dotkne země a svírá s ním úhel 30°. Vzdálenost mezi patou stromu a bodem, kde se vrchol dotýká země, je 8m. Najděte výšku stromu.
- Trojúhelníku 81595
Kus drátu je ohnutý do tvaru trojúhelníku. Dvě strany mají délku 24 palců a 21 palců. Úhel mezi těmito dvěma stranami je 55°. Jaká je délka třetí strany s přesností na setiny palce? Odpověď: Délka třetí strany je přibližně ____ palců. - Kosočtverec 83333
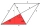Kosočtverec ABCD se stranou dlouhou 8 cm má úhlopříčku BD dlouhou 11,3 cm. Najděte úhel DAB. - Trojúhelníkový 81917 Tři domy tvoří trojúhelníkový tvar. Dům A je 50 stop od domu C a dům B je 60 stop od domu C. Úhel ABC je 80 stupňů. Nakreslete obrázek a najděte vzdálenost mezi A a B.
- Pravidelny osmiúhelník
Jedna strana pravidelného osmiúhelníku má 12 palců. Najděte apotém a jeho obsah. - -2√3/2=-π/3 80686
Nechť z = 2 - sqrt(3i). Najděte z6 a vyjádřete svou odpověď v pravoúhlém tvaru komplexního čísla. Jestliže z = 2 - 2sqrt(3 i), pak r = |z| = sqrt(2 ^ 2 + (- 2sqrt(3)) ^ 2) = sqrt(16) = 4 a theta = tan -2√3/2=-π/3
Vyřešte následující výpočet komplexních verzorů - 5,2∠58° - 1,6∠-40° a dejte odpověď v polární forměMáš úkol, nad kterým si lámeš alespoň 10 minut hlavu? Pošli nám úkol a my Ti ji zkusíme vypočítat. Řešení příkladů z matematiky.
