Vzdálenost 84361
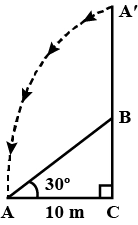
Strom se vlivem bouře zlomí a zlomená část se ohne tak, že se vrchol stromu dotkne země a svírá s ním úhel 30°. Vzdálenost mezi patou stromu a bodem, kde se vrchol dotýká země, je 8m. Najděte výšku stromu.
Správná odpověď:
Tipy na související online kalkulačky
Chcete proměnit jednotku délky?
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte si převody jednotek úhlů úhlové stupně, minuty, sekundy, radiány.
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte si převody jednotek úhlů úhlové stupně, minuty, sekundy, radiány.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
- aritmetika
- odmocnina
- planimetrie
- Pythagorova věta
- pravoúhlý trojúhelník
- trojúhelník
- goniometrie a trigonometrie
- tangens
Jednotky fyzikálních veličin:
Úroveň náročnosti úkolu:
Související a podobné příklady:
- Strom 5
Strom je zlomen ve výšce 4 metry nad zemí a vršek stromu se dotýká země ve vzdálenosti 5 od kmene. Vypočti původní výšku stromu. - Stožár
Stožár vysoký 32 metrů byl větrem zlomen tak, že se jeho vrchol dotýká země 16 metrů od paty stožáru. Ještě stojící část stožáru, ulomená část a země vytvářejí pravoúhlý trojúhelník. V jaké výšce byl stožár zlomen? - Vzdálenost 73594
Maggie z okna pozoruje auto a strom. Úhel sklonu auta je 45 stupňů a úhel stromu je 30 stupňů. Pokud je vzdálenost mezi autem a stromem 100 m, najděte vzdálenost Maggie od stromu. - Letadlo 3
Letadlo letělo 50 km kurzem 63°20' a pak 153°20' 140 km. Najděte vzdálenost mezi výchozím a koncovým bodem.
- Pozorovací 83872
Muž stojící na palubě lodi, která je 10 m nad hladinou vody, pozoruje vrchol kopce při úhlu elevace 60° a pozorovací úhel sklonu paty kopce je 30°. Najděte vzdálenost kopce od lodi a výšku kopce. - Javor
Vrchol stromu - javoru vidno ze vzdálenosti 3 m od kmene stromu z výšky 1,7 m pod úhlem 64°. Zjistěte výšku stromu. - Trojúhelníku 50281
Sestavte problém analytické geometrie, kde je třeba nalézt vrcholy trojúhelníku ABC: vrcholy tohoto trojúhelníku musí být body A (1,7) B (-5,1) C (5, -11). V uvedeném problému by se měly použít pojmy: vzdálenost od bodu k přímce, poměr dělení úsečky bodem
