Pozorovací 84154
Z bodu A na zemi je pozorovací úhel vrcholu 20 m vysoké budovy 45°. Na vrcholu budovy je vztyčená vlajka a pozorovací úhel vrcholu vlajkové tyče od A je 60°. Najděte délku vlajkové tyče a vzdálenost budovy od bodu A.
Správná odpověď:
Tipy na související online kalkulačky
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte si převody jednotek úhlů úhlové stupně, minuty, sekundy, radiány.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte si převody jednotek úhlů úhlové stupně, minuty, sekundy, radiány.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
- algebra
- vyjádření neznámé ze vzorce
- planimetrie
- pravoúhlý trojúhelník
- trojúhelník
- goniometrie a trigonometrie
- tangens
Jednotky fyzikálních veličin:
Úroveň náročnosti úkolu:
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1
Související a podobné příklady:
- Pozorovací 84353
Pozorovací úhel vrcholu věže od bodu A na zemi je 30°. Při přesunu na vzdálenost 20 m směrem k patě věže do bodu B se pozorovací úhel zvětší na 60°. Najděte výšku věže a vzdálenost věže od místa A . - Věž + stožár
Na vodorovné rovině je svislá věž s vlajkovou tyčí na jejím vrcholu. V bodě vzdáleném 9 m od nohy věže je úhel elevace horní a dolní části vlajkové tyče 60° a 30°. Najděte výšku stožáru vlajky. - Zaokrouhlete 81683
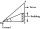Avanti se snaží nalézt výšku rádiové antény na střeše místní budovy. Stojí ve vodorovné vzdálenosti 21 metrů od budovy. Úhel elevace od jejího očí ke střeše (bod A) je 42° a úhel elevace od jejího očí k vrcholu antény (bod B) je 51°. Pokud jsou její oči 1 - Pozorovací 83872
Muž stojící na palubě lodi, která je 10 m nad hladinou vody, pozoruje vrchol kopce při úhlu elevace 60° a pozorovací úhel sklonu paty kopce je 30°. Najděte vzdálenost kopce od lodi a výšku kopce.
- Vypočítejte 6280
Chlapec o výšce 1,7 m stojí 30 m od vlajkové tyče na stejné úrovni. Všiml si, že úhel odchylky vrcholu vlajkové tyče je 30 stupňů. Vypočítejte výšku vlajkové tyče. - Předpokladu 84214
Ve výšce 60 m nad zemí létá drak. Šňůrka připevněná k drakovi je dočasně přivázána k bodu na zemi. Sklon šňůry se zemí je 60°. Najděte délku šňůry za předpokladu, že šňůry je našponovaná a není volná. - Pozorovací 84039
Dvaja muži sú na opačných stranách veže. Nameajú uhly elevácie (pozorovací) vrcholu veže jako 30° a druhý ako 45°. Ak je výška veže 50 m, nájdi vzdálenost medzi týmito dvoma mužmi.
