Povrch tělesa + Pythagorova věta - příklady a úlohy
Počet nalezených příkladů: 298
- Na válec
Na válec o průměru 4,6 cm nasaďte část koule tak, aby povrch této části byl 20 cm². Určete r koule ze které byl vrchlík seříznut. - Krychle
Jedna krychle je kouli vepsána a druhá opsána. Vypočítejte rozdíl objemů v obou krychlích, pokud rozdíl jejich povrchů je 231 dm². - Vrchol 9
Vrchol věže má tvar pravidelného šestibokého jehlanu. Podstavná hrana má délku 1,2 m, výška jehlanu je 1,6 m. Kolik metrů čtverečných plechu je potřeba na pokrytí vrcholu věže, je-li na spoje, překrytí a odpad zapotřebí 15% plechu navíc? - Kvádr težší
Kvádr má objem 32 cm³. Jeho plášť má dvojnásobný obsah než jedna ze čtvercových podstav. Jakou délku má tělesová úhlopříčka?
- Dřevená 3
Dřevená deska dlouhá 2,5m má pruřez tvaru pravidelného lichobežníku jehož rovnobežné strany májí delku 1,2dm a 8cm vyška lichobežníka je 3cm. Vypočtete: a) povrch desky pro vypočet spotřeby mořidla b) hmotnost desky je-li hustota dřeva je 600kg/m³ c) koli - 4-boký jehlan v2
Vypočítejte objem a povrch pravidelného čtyřbokého jehlanu, jeli obsah podstavy 20 cm². Odchylka boční hrany od roviny podstavy je 60 stupňů. - Kužel
Vypočítej objem a povrch kužele, pokud průměr podstavy je d = 14 cm a strana kužele svírá s rovinou podstavy úhel 34°24'. - Kužel S2V
Plášť kužele rozvinutý do roviny má tvar kruhové výseče se středovým úhlem 126° a obsahem 415 cm². Vypočítejte objem tohoto kužele. - Karnevalových 30781
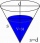Kolik dm² ozdobného papíru je potřeba ke zhotovení karnevalových čepic tvaru kužele pro 46 prvňáků, pokud obvod hlavy prvňáčka je 49 cm a výška čepice má být 33 cm. Na záhyby je nutné přidat 3% papíru?
- Věžička Věžička má tvar pravidelného čtyřbokého jehlanu s podstavnou hranou délky 0,8 m. Výška věžičky je 1,2 m. Kolik metrů čtverečných je potřeba na její pokrytí, počítáne-li na odpad 10% plechu navíc.
- Na louce
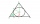Na louce přistála kosmická loď ve tvaru koule o průměru 6 m. Aby nepoutala pozornost, zakryli ji marťanci střechou ve tvaru pravidelného kužele. Jak vysoká bude tato střecha, aby spotřeba krytiny byla minimální? - Dopravní kužely
Čtyřicet stejných dopravních kuželů s průměrem podstavy d=3dm a výškou v=6dm máme natřít zvenčí oranžovou barvou (bez podstavy). Kolik korun zaplatíme za barvu, pokud na natření 1m² potřebujeme 50 cm³ barvy a 1l barvy stojí 80 Kč? - Věžička 2
Věžička má půdorys tvaru čtverce s délkou strany 5m. Střecha věžičky má tvar pravidelného čtyřbokého jehlanu (bez podstavy) s výškou 8m. Při rekonstrukci se bude střecha pokrývat novými taškami. Na 1 m² se spotřebuje 11 tašek. Na jedné paletě je uskladněn - Trojboký jehlan
Vypočítejte objem a povrch pravidelného trojbokého jehlanu, jehož výška je stejná jako délka hrany podstavy 10 cm.
- Iglu stan
Stan ve tvaru kužele je vysoký 3 m, průměr jeho podstavy je 3,2 m. a) Stan je vyroben je ze dvou vrstev materiálu. Kolik m² látky třeba na výrobu (včetně podlahy), pokud k minimálnímu množství třeba kvůli odpadu při stříhání přidat 20%? b) Kolik m³ vzduch - Jehlan
Urči povrch pravidelného čtyřbokého jehlanu, když je dán jeho objem V = 120 a úhel boční stěny s rovinou podstavy je α = 42° 30'. - Součet velikostí hran
Vypočtěte povrch kvádru, je-li dán součet velikostí jeho hran a+b+c=19 cm a velikost tělesové úhlopříčky u=13 cm. - Stan pro skauty
Stan pro skauty má dřevěnou obdélníkovou podsadu s rozměry 220 cm a 150 cm. Kolik plátna je třeba na střechu tvaru čtyřbokého jehlanu vysokého 170 cm? - Stříška
Pan Peter má nad studní plechovou stříšku tvaru kužele o výšce 101 cm a poloměru 189 cm. Stříška potřebuje natřít antikorozní barvou. Kolik kg barvy musí nakoupit, jestliže výrobce udává spotřebu 1kg na 4,3 m²?
Pana Radomíra při poslední bouřce postihlo neštěstí, na střechu tvaru pravidelného čtyřbokého jehlanu mu spadl strom a celou mu ji poničil. Střecha má podstavou délku hrany 8m a délku boční hrany 15m. Kolik m² střešní krytiny bude muset nakoupit?Máš úkol, nad kterým si lámeš alespoň 10 minut hlavu? Pošli nám úkol a my Ti ji zkusíme vypočítat. Řešení příkladů z matematiky.
