Vzdialenosť 84353

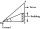
Pozorovací uhol vrcholu veže od bodu A na zemi je 30°. Pri presune na vzdialenosť 20 m smerom k päte veže do bodu B sa pozorovací uhol zväčší na 60°. Nájdite výšku veže a vzdialenosť veže od miesta A .

Správna odpoveď:

h =  17,3 m
x =  10 m

Postup správneho riešenia:

α=30 ∘ β=60 ∘ a=20 m  tg β = h:x = h/x tg α = h:(x+a) = h/(x+a)  x = h / tg β  = h / t1​ t1​=tgβ=tg60° =1,732051=1,73205 t2​=tgα=tg30° =0,57735  t2​⋅ (h/t1​+a) = h t2​⋅ h/t1​+a⋅ t2​ = h  h=t1​−t2​a⋅ t1​⋅ t2​​=1,7321−0,577420⋅ 1,7321⋅ 0,5774​=10 3​≐17,3205 m   Skuˊsˇka spraˊvnosti:  x=h/t1​=17,3205/1,7321=10 m α2​=π180°​⋅arctg(x+ah​)=π180°​⋅arctg(10+2017,3205​)=30 ∘ β2​=π180°​⋅arctg(xh​)=π180°​⋅arctg(1017,3205​)=60 ∘

Skúsiť iný príklad


Našiel si chybu či nepresnosť? Kľudne nám ju napíš.







Tipy na súvisiace online kalkulačky
Potrebujete pomôcť spočítať, vykrátiť či vynásobiť zlomky? Skúste našu zlomkovú kalkulačku.
Máte lineárnu rovnicu alebo sústavu rovníc a hľadáte jej riešenie? Alebo máte kvadratickú rovnicu?
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Vyskúšajte si prevody jednotiek uhlov uhlové stupne, minúty, sekundy, radiány.

Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:

Jednotky fyzikálnych veličín:

Úroveň náročnosti úlohy:


 
Odporúčame k tejto úlohe z matematiky si pozrieť toto výukové video: video1   video2   video3   video4   video5

Súvisiace a podobné príklady: