The angle 9
The angle of elevation of the top of a tower from a point A on the ground is 30°. On moving a distance of 20 m towards the foot of the tower to a point B, the angle of elevation increases to 60°. Find the height of the tower and the distance of the tower from A .
Correct answer:

Tips for related online calculators
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
You need to know the following knowledge to solve this word math problem:
- algebra
- equation
- system of equations
- expression of a variable from the formula
- planimetrics
- right triangle
- triangle
- goniometry and trigonometry
- tangent
- arctangent
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Tower + pole
 On the horizontal plane, there is a vertical tower with a flag pole on its top. At a point 9 m away from the foot if the tower, the angle of elevation of the top and bottom of the flag pole are 60°and 30° respectively. Find the height of the flag pole.
On the horizontal plane, there is a vertical tower with a flag pole on its top. At a point 9 m away from the foot if the tower, the angle of elevation of the top and bottom of the flag pole are 60°and 30° respectively. Find the height of the flag pole. - Elevation of the tower
 We can see the top of the tower standing on a plane from a certain point A at an elevation angle of 39°25''. If we come towards its foot 50m closer to place B, we can see the top of the tower from it at an elevation angle of 56°42''. How tall is the tower
We can see the top of the tower standing on a plane from a certain point A at an elevation angle of 39°25''. If we come towards its foot 50m closer to place B, we can see the top of the tower from it at an elevation angle of 56°42''. How tall is the tower - Angle of elevation
 From a point A on the ground, the angle of elevation of the top of a 20 m tall of a building is 45°. A flag is hoisted at the top of the building and the angle of elevation of the top of the flagstaff from A is 60°. Find the length of the flagstaff and th
From a point A on the ground, the angle of elevation of the top of a 20 m tall of a building is 45°. A flag is hoisted at the top of the building and the angle of elevation of the top of the flagstaff from A is 60°. Find the length of the flagstaff and th - A radio antenna
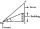 Avanti is trying to find the height of a radio antenna on the roof of a local building. She stands at a horizontal distance of 21 meters from the building. The angle of elevation from her eyes to the roof (point A) is 42°, and the angle of elevation from
Avanti is trying to find the height of a radio antenna on the roof of a local building. She stands at a horizontal distance of 21 meters from the building. The angle of elevation from her eyes to the roof (point A) is 42°, and the angle of elevation from
- Two men 2
 Two men are on opposite sides of a tower. They measure the angles of elevation of the top of the tower as 30° and 45°, respectively. If the height of the tower is 50 m, find the distance between the two men.
Two men are on opposite sides of a tower. They measure the angles of elevation of the top of the tower as 30° and 45°, respectively. If the height of the tower is 50 m, find the distance between the two men. - A tree 3
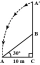 A tree breaks due to storm and the broken part bends so that the top of the tree touches the ground making an angle 30° with it. The distance between the foot of the tree to the point where the top touches the ground is 8 m. Find the height of the tree.
A tree breaks due to storm and the broken part bends so that the top of the tree touches the ground making an angle 30° with it. The distance between the foot of the tree to the point where the top touches the ground is 8 m. Find the height of the tree. - A man 23
 A man standing on the deck of a ship, which is 10 m above the water level, observes the angle of elevation of the top of a hill as 60°, and angle of depression of the base of the hill is 30°. Find the distance of the hill from the ship and the height of t
A man standing on the deck of a ship, which is 10 m above the water level, observes the angle of elevation of the top of a hill as 60°, and angle of depression of the base of the hill is 30°. Find the distance of the hill from the ship and the height of t
