Kvetinový záhon
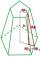
Kvetinový záhon má tvar zrezaného ihlana, pričom hrana dolnej podstavy a= 10 m, hornej podstavy b= 9 m a odchýlka počnej hrany od podstavy je alfa= 45°. Aký objem zemniny je potrebný navýšiť na tento záhon? Koľko sadeníc je možné vysadiť, ak 1m2= 100 sadeníc?
Správna odpoveď:
Tipy na súvisiace online kalkulačky
Potrebujete pomôcť spočítať, vykrátiť či vynásobiť zlomky? Skúste našu zlomkovú kalkulačku.
Viete objem a jednotku objemu a chcete premeniť jednotku objemu?
Chcete zaokrúhliť číslo?
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Vyskúšajte si prevody jednotiek uhlov uhlové stupne, minúty, sekundy, radiány.
Viete objem a jednotku objemu a chcete premeniť jednotku objemu?
Chcete zaokrúhliť číslo?
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Vyskúšajte si prevody jednotiek uhlov uhlové stupne, minúty, sekundy, radiány.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Súvisiace a podobné príklady:
- Kvetinový záhon 3
Kvetinový záhon má tvar pravidelného 4-bokého ihlanu. Hrana dolnej podstavy je 10m, hornej podstavy je 9m. Odchýlka bočnej steny od podstavy je 45 stupňov. Koľko sadenia treba nakúpiť, ak na vysadenie 1m štvorcového ich treba 90? - Zrezaný ihlan 2
Vypočítajte objem pravidelného šesťbokého zrezaného ihlana, ak je dĺžka hrany dolnej podstavy 30 cm, hornej podstavy 12 cm a ak dĺžka bočnej hrany je 41 cm. - Kosý hranol
Aký objem má štvorboký kosý hranol s podstavnými hranami o dĺžke a = 1m, b = 1,1m, c = 1,2 m, d = 0,7m, ak bočná hrana s dĺžkou h = 3,9m má odchýlku od podstavy 20° 35 'a hrany a, b zvierajú uhol 50,5°. - Kvetinový 5
Kvetinový záhon má tvar rovnorameného trojuholníka so základňou 25m a ramenami 30m dlhými. Vypočitaj, najviac koľko kvetov môžeme na tento záhon vysadiť, ak predpokladáme, že jeden kvet potrebuje asi 8 dm štvorcových plochy. Výsledok zaokrúhli na desiatky
- Pyramída v Gize
Veľká pyramída v Gize má tvar pravidelného štvorbokého ihlana. Podstavná hrana má dľžku 227 m a výška pyramídy je 140 m. Akú hmotnosť má kameň, ktorý bol potrebný na stavbu tejto pyramídy, ak hmotnosť 1 m³ kameňa je 2,5 t? - Objem 38
Objem zrezaného kužeľa je V=38000π cm³. Polomer dolnej podstavy je o 10 cm väčší, ako polomer hornej podstavy. Určte polomer podstáv, ak výška v=60 cm. - Pravidelného 21523
Vypočítajte povrch a objem pravidelného štvorbokého ihlana, ak je hrana dolnej podstavy 18 cm a hrana hornej podstavy 15 cm. Stenová výška je 9 cm.
