Štvoruholník
Ukážte, že štvoruholník s vrcholmi P1 (0,1), P2 (4,2) P3 (3,6) P4 (-5,4) má dva pravé trojuholníky.
Správna odpoveď:

Tipy na súvisiace online kalkulačky
Chcete premeniť jednotku dĺžky?
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
- geometria
- analytická geometria
- aritmetika
- odmocnina
- planimetria
- Pytagorova veta
- pravouhlý trojuholník
- trojuholník
- lichobežník
- kosoštvorec
- uhlopriečka
- obdĺžnik
- rovnobežník
- štvoruholník
Jednotky fyzikálnych veličín:
Úroveň náročnosti úlohy:
Súvisiace a podobné príklady:
- Body - vrcholy
 Ukážte, že body P1 (5,0), P2 (2,1) a P3 (4,7) sú vrcholy pravého trojuholníka.
Ukážte, že body P1 (5,0), P2 (2,1) a P3 (4,7) sú vrcholy pravého trojuholníka. - Vrcholy trojuholníka
 Ukážte, že body D (2,1), E (4,0), F (5,7) sú vrcholy pravouhlého trojuholníka.
Ukážte, že body D (2,1), E (4,0), F (5,7) sú vrcholy pravouhlého trojuholníka. - Kolineárne body
 Ukážte, že body A (-1,3), B (3,2), C (11,0) sú kolineárne (ležia na jednej priamke).
Ukážte, že body A (-1,3), B (3,2), C (11,0) sú kolineárne (ležia na jednej priamke). - MO Z6-I-3 2022
 Magda si vystrihla dva rovnaké rovnoramenné trojuholníky, z ktorých každý mal obvod 100 cm. Najprv z týchto trojuholníkov zložila štvoruholník tak, že ich k sebe priložila ramenami. Potom z nich zložila štvoruholník tak, že ich k sebe priložila základňami
Magda si vystrihla dva rovnaké rovnoramenné trojuholníky, z ktorých každý mal obvod 100 cm. Najprv z týchto trojuholníkov zložila štvoruholník tak, že ich k sebe priložila ramenami. Potom z nich zložila štvoruholník tak, že ich k sebe priložila základňami
- Štvoruholník 4
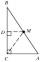
 Štvoruholník ABCD je zložený z dvoch pravouhlých trojuholníkov ABD a BCD. Pre dĺžky strán platí: |AD| = 3cm, |BC| = 12cm, |BD| = 5cm. Koľko centimetrov štvorcových má štvoruholník ABCD? Uhly DAB a DBC sú pravé.
Štvoruholník ABCD je zložený z dvoch pravouhlých trojuholníkov ABD a BCD. Pre dĺžky strán platí: |AD| = 3cm, |BC| = 12cm, |BD| = 5cm. Koľko centimetrov štvorcových má štvoruholník ABCD? Uhly DAB a DBC sú pravé. - Lichobežník
 Z obdĺžnikovej dosky sme odrezali dva trojuholníky tak, že vzniknutý štvoruholník- lichobežník s rovnakými dĺžkami ramien má obsah 32 cm² a jedna jeho základňa je dvakrát dlhšia ako druhá. Aký obsah majú spolu dva trojuholníky, ktoré tvoria odpad?
Z obdĺžnikovej dosky sme odrezali dva trojuholníky tak, že vzniknutý štvoruholník- lichobežník s rovnakými dĺžkami ramien má obsah 32 cm² a jedna jeho základňa je dvakrát dlhšia ako druhá. Aký obsah majú spolu dva trojuholníky, ktoré tvoria odpad? - Pravdepodobnosť
 V tabuľke sú informácie o počte žiakov podľa počtu súrodencov: Počet súrodencov 0 1 2 3 a viac Počet žiakov 50 50 72 28 Aká je pravdepodobnosť, že náhodne vybraný žiak má práve dvoch súrodencov?
V tabuľke sú informácie o počte žiakov podľa počtu súrodencov: Počet súrodencov 0 1 2 3 a viac Počet žiakov 50 50 72 28 Aká je pravdepodobnosť, že náhodne vybraný žiak má práve dvoch súrodencov?
