Súčet vektorov
Veľkosť vektora u je 4, vektora v je 3. Vektory zvierajú uhol 45°. Aká je veľkosť vektora u+v?
Správna odpoveď:
Tipy na súvisiace online kalkulačky
Dva vektory určené veľkosťami a vzájomným uhlom sčíta naša kalkulačka sčítania vektorov.
Kosínusovú vetu priamo používa kalkulačka SUS trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Kosínusovú vetu priamo používa kalkulačka SUS trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
- geometria
- analytická geometria
- vektor
- planimetria
- trojuholník
- kosínusová veta
- goniometria a trigonometria
- kosínus
Jednotky fyzikálnych veličín:
Úroveň náročnosti úlohy:
Odporúčame k tejto úlohe z matematiky si pozrieť toto výukové video: video1
Súvisiace a podobné príklady:
- Vektory 5
Polohový vektor hmotného bodu, ktorý sa pohybuje v rovine, je možné v zavedenej vzťažnej sústave vyjadriť vzťahom: r(t) = (2t + 3t²; 6t + 3), kde t je čas v sekundách a súradnice vektora sú v metroch. Vypočítajte: a) aká je poloha hmotného bodu v čase t = - Vektory
Vektor a má súradnice (9; -1) a vektor b má súradnice (-13; 6). Ak vektor c= b-a, aká je veľkosť vektora c? - Vektory - základné operácie
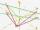Dané sú body A[-13;-18] B[20;9] C[-18; -3] a D[-14;-10] a. Určite súradnice vektorov u=AB v=CD s=DB b. Vypočítajte súčet vektorov u+v c. Vypočítajte rozdiel vektorov u-v d. Určite súradnice vektora w=-2.u - Polohový 3
Polohový vektor hmotného bodu, ktorý sa pohybuje v rovine, je možné v zavedenej vzťažnej sústave vyjadriť vzťahom: r(t) = (t2+ 2t + 1 ; 2t + 1), kde t je čas v sekundách a súradnice vektora sú v metroch. Vypočítajte: a) aká je poloha hmotného bodu v čase
- Polohový 2 Polohový vektor hmotného bodu, ktorý sa pohybuje v rovine, je možné v zavedenej vzťažnej sústave vyjadriť vzťahom: r(t) = (1 + 5t + 2t² ; 3t + 1), kde t je čas v sekundách a súradnice vektora sú v metroch. Vypočítajte: a) aká je poloha hmotného bodu v čas
- Polohový vektor
Polohový vektor hmotného bodu, ktorý sa pohybuje v rovine, je možné v zavedenej vzťažnej sústave vyjadriť vzťahom: r(t) = (6t²+ 4t ; 3t + 1) kde t je čas v sekundách a súradnice vektora sú v metroch. Vypočítajte: a) aká je poloha hmotného bodu v čase t = - Kartézskej 59863
Je daný koncový bod vektora, ktorý je umiestnený v počiatku kartézskej sústavy Oxy. Určite súradnice vektora, jeho veľkosť a načrtnite ho: P[3,4] ; Q[-2,7] ; S[-5,-2] . .. tj Vektory PO, QO, SO
