Planimetrie - slovní úlohy a příklady - strana 135 z 174
Počet nalezených příkladů: 3463
- Trojuholníka 40961
Pravoúhlý trojúhelník ABC má odvěsny a = 5 cm, b = 8 cm. K němu podobný trojúhelník A'B'C' je 2,5krát menší. Vypočítej kolik procent z obsahu trojúhelníku ABC tvoří obsah trojúhelníku A'B'C'. - Vzdálenosti 79974
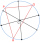Na obrázku jsou znázorněny tři obce A, B, C a jejich vzájemné vzdušné vzdálenosti. Nová přímočará želežniční trať má být postavena tak, aby ze všech obcí bylo k trati stejně daleko a aby tato vzdálenost byla nejmenší možná. Jak daleko budou od trati? a = - Trojúhelníku 80745
Obsah pravoúhlého trojúhelníku KLM s pravým úhlem u vrcholu L je 60 mm čtverečních a jeho odvěsna k má délku 10 mm. Trojúhelníky KLM a RST jsou podobné, poměr podobnosti je k=2,5 . Vypočítej obsah trojúhelníku RST. - Tečna
Je dána kružnice k se středem S a poloměrem 3,5cm. Vzdálenost přímky p od středu je 6 cm. Sestrojte tečnu kružnice n, která je kolmá na přímku p
- Čtverec
Narýsujte čtverec o hraně a= 4cm. Vyznačte střed souměrnosti S a všechny osy souměrnosti. Kolik os souměrnosti má? Zapište. - Dvaja
Dvě přímé čáry kříží v pravém úhlu. Dva lidé začínají současně v místě křižovatky. John jde rychlostí 4 km/h po jedné cestě a Peter jede rychlostí 8 km/h po druhé cestě. Jak dlouho bude trvat, než budou vzdálený 20√5 km od sebe? - Kolmá tyč
Metrová tyč kolmá k zemi vrhá stín dlouhý 40 cm, dům vrhá stín dlouhý 6 metrů. Jaká je výška domu? - Rovnoramenný lichoběžník
Rovnoramenný lichoběžník ABCD o základnách délky |AB| = 6 cm, |CD| = 4 cm je diagonálami protínajícími se v bodě S rozdělen na 4 trojúhelníky. Jakou část plochy daného lichoběžníka zaujímají trojúhelníky ABS a CDS? - Do kruhu
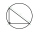Do kruhu s průměrem 20cm byl vepsán pravoúhlý trojúhelník, jehož přepona je průměrem kruhu má co největší obsah. Vypočítej obsah tohoto trojúhelníku.
- Slneční lúče
Devíti metrový topol vrhá stín 16,2m. Jak dlouhý stín vrhá ve stejnou dobu Pepík, jestliže je vysoký 1,4m? - Člověk 7838 Člověk vysoký 1,65m vrhá stín dluhy 1,25m. Jak vysoký je strom jehož stín je dluhy 2,58 m?
- Dvoumetrová 3473
Strom s neznámou výškou vrhá stín dlouhý 18 m, v době, kdy dvoumetrová tyč vrhá stín 2,4m. Jak vysoký je strom? - Svislá
Svislá metrová tyč vrhá stín 150 cm dlouhý. Vypočtěte výšku sloupu, jehož stín je ve stejném okamžiku 36 m dlouhý. - Šestiúhelník lomeno
Pravidelný šestiúhelník rozdělte úsečkami na devět zcela shodných dílů; žádný z nich nesmí být v zrcadlovém zobrazení (jednotlivé díly mohou být pouze libovolně pootočeny).
- Dálka
Karel a Eva stojí před svým domem, Karel šel do školy směrem na jih rychlostí 5,4 km/h, Eva jela do obchodu na kole východním směrem rychlostí 21,6 km/h. Jak daleko budou od sebe za 10 minut? - Délka 15
Délka stínu lípy je 429cm. Délka stínu metrové týče je 78cm. Vypočítej výšku lípy. - Pohybovalo 62844
Těleso o hmotnosti 4 kg narazilo na překážku rychlostí 10 m/s. Po srážce se těleso dále pohybovalo rychlostí 6 m/s, přičemž směr této rychlosti byl kolmý na směr rychlosti před srážkou. Určete a) změnu velikosti rychlosti a hybnosti tělesa a b) velikost z - Vektor
Vektor u=(3,9,u3) a velikost vektoru u=12. Kolik je u3? - Poloměrem 6500
Narýsuj úsečku KL=55mm. Narýsuj kružnici k se středem K a poloměrem 4cm. Vyznačuj body tak, aby patřily kružnici a spojuj je s bodem L.
Určete rovnici kružnice, která je množinou všech bodů roviny, které mají od bodu [3,7] dvakrát větší vzdálenost než od bodu [0,1].Máš úkol, nad kterým si lámeš alespoň 10 minut hlavu? Pošli nám úkol a my Ti ji zkusíme vypočítat. Řešení příkladů z matematiky.
