Rovnoramenný 3uholník dôkaz
Použitím kosínovej vety dokážte, že v rovnoramennom trojuholníku ABC so základňou AB platí, že c=2a cos α.
Správna odpoveď:
Tipy na súvisiace online kalkulačky
Vypočet rovnoramenného trojuholníka.
Kosínusovú vetu priamo používa kalkulačka SUS trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Kosínusovú vetu priamo používa kalkulačka SUS trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Jednotky fyzikálnych veličín:
Téma:
Úroveň náročnosti úlohy:
Odporúčame k tejto úlohe z matematiky si pozrieť toto výukové video: video1
Súvisiace a podobné príklady:
- Maturitný - RR - základňa
V rovnoramennom trojuholníku ABC so základňou AB platí ∠BAC = 20°, AB = 4. Os vnútorného uhla pri vrchole B pretína stranu AC v bode P. Vypočítajte dĺžku úsečky AP. Výsledok uveďte s presnosťou na dve desatinné miesta. - V rovnoramennom 4
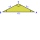V rovnoramennom trojuholníku ABC so základňou AB; A[-3,4]; B[1,6] leží vrchol C na priamke 5x – 6y – 16 =0. Vypočítajte súradnice vrcholu C. - Dôkaz - MO - C – I – 3
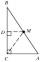Päta výšky z vrcholu C v trojuholníku ABC delí stranu AB v pomere 1:2. Dokážte, že pri zvyčajnom označení dĺžok strán trojuholníka ABC platí nerovnosť 3|a-b| < c. - Trojuholník PRT
V rovnoramennom pravouhlom trojuholníku ABC s pravým uhlom pri vrchole C platí o súradniciach bodov: A (-1, 2); C (-5, -2) Vypočítajte dĺžku strany AB.
- Trojuholníka 81019
V pravouhlom trojuholníku ABC (AB je prepona) platí a : b = 24 : 7 a výška na stranu c = 12,6 cm. Vypočítajte dĺžky strán trojuholníka ABC. - V rovnoramennom 5
V rovnoramennom trojuholníku ABC je t'ažisko T vzdialené 2 cm od základne AB. Stredná priečka rovnobežná so stranou AB meria 4cm. Aký obsah má trojuholník ABC? - Rovnoramenný IV
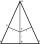V rovnoramennom trojuholníku ABC je |AC|=|BC| = 13. |AB| = 10. Vypočítajte polomer vpísanej (r) a opísanej (R) kružnice.
