Podstava RR licho
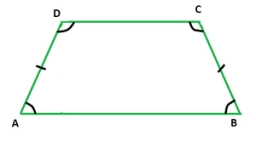
Podstavou hranolu je rovnoramenný lichoběžník ABCD se
základnami AB = 12 cm, CD = 9 cm. Úhel při vrcholu B je 48° 10'.
Určete objem a porch hranolů, je-li jeho výška 35 cm.
Vaše odpověď:
základnami AB = 12 cm, CD = 9 cm. Úhel při vrcholu B je 48° 10'.
Určete objem a porch hranolů, je-li jeho výška 35 cm.
Vaše odpověď:
Tipy na související online kalkulačky
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Víte objem a jednotku objemu a chcete proměnit jednotku objemu?
Vypočet rovnoramenného trojúhelníku.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte si převody jednotek úhlů úhlové stupně, minuty, sekundy, radiány.
Víte objem a jednotku objemu a chcete proměnit jednotku objemu?
Vypočet rovnoramenného trojúhelníku.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte si převody jednotek úhlů úhlové stupně, minuty, sekundy, radiány.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
algebraaritmetikastereometrieplanimetriegoniometrie a trigonometrieJednotky fyzikálních veličinÚroveň náročnosti úkolu
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1
Související a podobné příklady:
- V rovnoramenný lichoběžník
V rovnoramenném lichoběžníku ABCD jsou dány jeho základny AB=20 cm, CD=12 cm a ramena AD=BC=8 cm. Určete jeho výšku a úhel alfa při vrcholu A. - Lichoběžník - RR
Daný je rovnoramenný lichoběžník ABCD se základnami 10 cm a 14 cm. Výška lichoběžníku je 6 cm. Určete vnitřní úhly lichoběžníku. - Rovnoramenný lichoběžník
V rovnoramenném lichoběžníku ABCD, AB||CD, je |CD| = c = 10 cm, výška v = 4 cm, |CAB| = 33°. Vypočítej obsah lichoběžníku. - Vypočítejte 258
Vypočítejte objem a povrch hranolu s lichoběžníkovou podstavou a výškou 9 cm. Podstava je rovnoramenný lichoběžník se základnami o délkách 3 cm a 6 cm a rameny délky 2,5 cm. Výška podstavy je 2 cm. - Čtyřboký hranol 6
Vypočítej povrch čtyřbokého hranolu ABCDA'B'C'D' s lichoběžníkovou podstavou ABCD. Výška hranolu je 12 cm; údaje o lichoběžníku ABCD: délka základny AB je 8 cm, délka základny CD je 3 cm, délka ramene BC je 4 cm a délka úhlopříčky AC je 7 cm. Napovíme: Na - Úhly trojúhelníku v lichoběžníku
Daný je rovnoramenný lichoběžník ABCD, ve kterém platí |AB|= 2|BC|= 2|CD|= 2|DA|. Na jeho straně BC je bod K takový, že |BK| = 2|KC|, na jeho straně CD je bod L takový, že |CL|= 2|LD|, a na jeho straně DA je bod M takový, že |DM|= 2|MA|. Určete velikosti - Úhlopříčka
Určete délku úhlopříčky BD v pravoúhlém lichoběžníku ABCD s pravým úhlem při vrcholu A, když /AD/=8,1 cm a úhel DBA je 42°
