Pravouhlý trojuholník + kúžeľ - príklady a úlohy
Počet nájdených príkladov: 112
- Pravidelný 4B ihlan
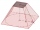Vypočítajte povrch a objem pravidelného štvorbokého komolého ihlana, ak sú hrany podstavy 87 cm a 64 cm a stenová výška je 49 cm. - Do nádoby 2
Do nádoby tvaru rovnostranného kužeľa, ktorého podstava má polomer r = 6 cm nalejeme toľko vody, že sa naplní jedna tretina objemu kužeľa. Do akej výšky bude siahať voda, ak kužeľ obrátime hore dnom? - Rotačné 8
Rotačné teleso vzniklo rotáciou rovnostranného trojuholníka s dĺžkou strany a=2 cm okolo jednej z jeho strán. Vypočítajte objem tohoto rotačného telesa. - Vypočítajte 15093
Nádoba tvaru kužeľa s priemerom dna 60cm a bočnou stranou dĺžky 0,5m je úplne naplnená vodou. Vodu prelejeme do nádoby, ktorá má tvár valca o polomere 3dm a výške 20cm. Bude valec pretekať, alebo naopak nebude plný? Vypočítajte koľko vody pretečie, alebo
- Stan iglu
Stan v tvare kužeľa je vysoký 3 m, priemer jeho podstavy je 3,2 m. a) Stan je vyrobený je z dvoch vrstiev materiálu. Koľko m² látky treba na výrobu (vrátane podlahy), ak k minimálnemu množstvu treba kvôli odpadu pri strihaní pridať 20 %? b) Koľko m³ vzduc - Guľa a kúžel
Do gule s polomerom G = 41 cm vpíšte kužel s najväčším objemom. Aký je tento objem a aké sú rozmery kužela? - Rotačného 28501
Do ktorého z vrecúšok v tvare plášťa rotačného kužeľa sa zmestí väčšie množstvo praženej kukurice? Prvé vrecko má výšku 20 cm a dĺžka jeho strany je 24 cm, druhé vrecko má polomer podstavy 10 cm a výšku 25 cm. - Cukrárskej 7318
Cukrárka potrebuje z cukrárskej hmoty v tvare gule o polomere 25cm vyrezať ozdobu v tvare kužeľa. Určte polomer podstavy ozdoby a (a výšku h) tak, aby sa na výrobu ozdoby použilo čo najviac hmoty. - Terwilliker 75264
Hromada soli bola uložená v tvare kužeľa. Pán Terwilliker vie, že hromada je 20 stôp vysoká a 102 stôp v obvode na základni. Aká plocha kónickej plachty (veľký kus materiálu) je potrebná na zakrytie hromady?
- Štvorcových 23801
Správca hradu sa pokúša odhadnúť, koľko štvorcových metrov plechu bude približne treba na novú strechu veže. Strecha má tvar kužeľa. Správca hradu vie, že priemer veže je 4,6 metra a výška je 5,2 metra. Koľko štvorcových metrov strecha meria? - Priemer
Priemer základne pravoúhleho kužeľa je 16 cm a jeho šikmá výška je 12 cm. A. ) Zistite kolmú výšku kužeľa na 1 desatinné miesto. B. ) Nájdite objem kužeľa a prepočítajte ho na 3 významné číslo. Použite pi = 3,14 - Kužeľ 20
Vypočítajte objem a plochu kužeľa, ktorého výška je 10 cm a v osovom reze zviera so stenou kužeľa uhol 30 stupňov. - Koľko 61
Koľko m² medeného plechu treba na výmenu strechy veže kužeľovitého tvaru, ktorej priemer je 13 metrov a výška 24 metrov, ak na zahnutie a odpad počítame 8 % materiálu? - Strecha 9
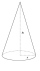Strecha hradnej veže má tvar kúžeľa s priemerom podstavy 12 m a výškou 8m. Koľko eur zaplatíme za pokrytie strechy, ak 1m štvorcový krytiny stojí 3,5 eura?
- Osový 6
Osový rez kužeľa je rovnoramenný trojuholník, v ktorom je pomer priemeru kužeľa a steny kužeľa 2:3. Vypočítajte jeho objem, ak viete, že jeho plocha je 314 cm štvorcových. - Tienidlo
Tienidlo v tvare kužeľa má priemer 30 cm a výšku 10 cm. Koľko cm² materiálu budeme potrebovať, ak počítame 10% na odpad? - Odchýlka podstavy a bočnej strany
Povrch rotačného kužeľa je 30 cm2, obsah jeho plášťa je 20 cm². Vypočítajte odchýlku strany tohto kužeľa od roviny podstavy. - Stredový uhol Plášť kužeľa s polomerom podstavy 20 cm a výškou 50 cm sa rozvinie do kruhového výseku. Aký veľký je stredový uhol tohto výseku ?
- Rotačné telesá
Rotačný kužeľ a rotačný valec majú rovnaký objem 180 cm³ a rovnakú výšku v = 15cm. Ktoré z týchto dvoch telies má väčší povrch?
Na lúke pristála kozmická loď v tvare gule s priemerom 6 m. Aby nepútali pozornosť, zakryli ju Marťankovia strechou v tvare pravidelného kužeľa. Ako vysoká bude táto strecha, aby spotreba krytiny bola minimálna?Máš úlohu, nad ktorou si lámeš aspoň 10 minút hlavu? Pošli nám úlohu a my Ti ju skúsime vypočítať. Riešenie príkladov z matematiky.
