Úměra, poměr + vyjádření neznámé ze vzorce - příklady a úlohy - poslední strana
Počet nalezených příkladů: 239
- Pumpy
Pumpou, která čerpá vodu rychlostí 3,5 litru za sekundu, se voda ze stavební jáma vyčerpá za 35 minut. a) Zjisti, za kolik minut by se voda z jámy vyčerpala pumpou, která čerpá 7,4 litru vody za sekundu. b) Jakou rychlost čerpání by musela mít pumpa, aby - RR trojúhelník
Vypočítej obsah rovnoramenného trojúhelníku KLM, jestliže pro délky jeho stran platí k:l:m = 4:4:3 a má obvod 377 mm. - Posloupnost
Najděte společný poměr (tzv. kvocient, resp. koeficient) posloupnosti 4, 2, 1, 0,5, 0,25 . Poměr zapište jako desetinné číslo zaokrouhleno na desetiny. - Kužel a poměr
Rotační kužel má výšku 58 cm a poměr podstavy k plášti je 9:13. Vypočítej podstavu a plášť (obsahy).
- Kvádr
Kvádr má povrch 1819 cm², délky jeho hran jsou v poměru 5:1:4. Vypočítej objem kvádru. - Kmen
Vypočítejte průměr kmene stromu s obvodem 125 cm. - Ťěžnice
Těžiště trojúhelníku QRS je vzdálené od vrcholu S 66 cm. Vypočítejte délku těžnice, která začínajúna vrcholem S. - Pravoúhlý trojúhelník
Pro odvěsny pravoúhlého trojúhelníku platí a:b = 7:8. Přepona má délku 88 cm. Vypočítejte obvod a obsah tohoto trojúhelníku. - Zvětšení koule
Kolikrát se zvětší objem koule, jestliže její priemer se zvětší 7×?
- Obdélníkového 84358
Délka a šířka obdélníkového parku jsou v poměru 8:5. Cesta, široká 1,5 m, vedoucí po celé vnější části parku má rozlohu 594 m². Najděte rozměry parku. - Nejmenší 84354
Jaké nejmenší číslo je třeba přidat ke každému z čísel 6, 15, 20 a 43, aby byly úměrné? - Rovnostranný v kruhu
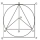Do čtverce je vepsán kruh. Do tohoto kruhu je vepsán rovnostranný trojúhelník se stranou 4√3. Najděte délku úhlopříčky čtverce. - Protisměr - vlaky
Dva vlaky jedoucí v protisměru obejdou muže stojícího na nástupišti za 27 vteřin a 17 vteřin a křižují se za 23 vteřin. Najděte poměr jejich rychlostí. - Vzdálenosti 83774
Rychlosti tří aut jsou v poměru 2:3:4. Jaký je poměr času, který tato auta potřebují k ujetí stejné vzdálenosti?
- Nejstarší 83764
Průměrný věk skupiny čtyř mužů, jejichž věk je v poměru 2:3:4:5 je 42 let. Jaký je věk nejstarší osoby z této skupiny? - Poměr základen
Jaký je poměr základen dvou trojúhelníků, když poměr jejich výšek je 3:4 a poměr jejich obsahů je 4:3? - Odpovídajícími 81967
Najděte poměr mezi dvěma obvody, dvěma oblastmi a dvěma odpovídajícími apotémy dvou pravidelných šestiúhelníků, jejichž strany jsou 2 3/4 palce a 4 1/8 palce. - Zůstalo 81775
Ve spíži byl stejný počet mrkve, rajčat a zelí. Yiguo použil 49 mrkví a trochu rajčat a trochu zelí. Rajčat zůstalo 3x více než zelí. Zůstalo o 16 méně mrkve než rajčat. Zůstalo celkem 117 mrkví, rajčat a zelí. Kolik mrkve bylo nejprve ve spíži? - X:14=28:196 81268
Riešte rovnice s dvěma poměry: x:14=28:196
Máš úkol, nad kterým si lámeš alespoň 10 minut hlavu? Pošli nám úkol a my Ti ji zkusíme vypočítat. Řešení příkladů z matematiky.
