Pythagorova věta - slovní úlohy a příklady - strana 51 z 72
Počet nalezených příkladů: 1422
- Plášť 8
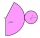Plášť kužele je vytvořen svinutím kruhové úseče o poloměru 1. Pro jaký středový úhel dané kruhové výseče bude objem vzniklého kužele maximální? - Vzdálenost bodů
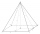Je dán pravidelný čtyřboký jehlan ABCDV, ve kterém AB = a = 4 cm a v = 8 cm. Nechť S je střed CV. Vypočítejte vzdálenost bodů A a S. - Správce hradu
Správce hradu se pokouší odhadnout, kolik čtverečných metrů plechu bude přibližně třeba na novou střechu věže. Střecha má tvar kužele. Správce hradu ví, že průměr věže je 4,6 metru a výška je 5,2 metru. Kolik čtverečných metrů střecha měří? - Nádrž
Nádrž má tvar pravidelného osmibokého hranolu bez horní podstavy. Podstavná hrana má a = 3m, boční hrana b = 6m. Kolik plechu třeba na zhotovení nádrže? Neberte v úvahu ztráty, ani tloušťku plechu.
- Kvádr
Kvádr má objem 40 cm³. Kvádr má celkovou plochu 100 cm čtverečních. Jedna hrana kostky má délku 2 cm. Najděte délku úhlopříčky kvádru. Dejte svou odpověď správně na 3 desetinná místa. - Rotační telesa
Rotační kužel a rotační válec mají stejný objem 180 cm³ a stejnou výšku v=15cm. Které z těchto dvou těles má větší povrch? - Podstava
Podstavou kvádru je obdélník se stranou 7,5 cm a úhlopříčkou 12,5 cm. Objem kvádru je V = 0,9 dm³. Vypočtěte povrch kvádru. - Trojboký hranol
Rovina, která prochází hranou AB a středem hrany CC' pravidelného trojbokého hranolu ABCA'B'C', svírá s podstavou úhel 46 stupňů, |AB| = 12 cm. Vypočítejte objem hranolu. - Rovnostranného 81142
Rotační těleso vzniklo rotací rovnostranného trojúhelníku o délce strany a=2 cm kolem jedné z jeho stran. Vypočítejte objem tohoto rotačního tělesa.
- Zaplatíme 33361
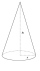Střecha hradní věže má tvar kužele o průměru podstavy 12 m a výšce 8m. Kolik eur zaplatíme za pokrytí střechy, pokud 1m čtvereční krytiny stojí 3,5 eura? - Pravidelného 27601
Střecha domu má tvar pravidelného čtyřbokého jehlanu vysokého 4 m s hranou podstavy o velikosti 100dm. Vypočítejte, kolik m² střešní krytiny je zapotřebí k pokrytí střechy, pokud bereme v úvahu 30% krytiny navíc k překrytí. - Pravidelného 6610
Plášť rotačního válce je 4krát větší než obsah jeho podstavy. Určete objem pravidelného trojbokého hranolu, který je ve válci vepsán. Poloměr podstavy válce je 10 cm. - Kruhového 4690
Plášť kužele s poloměrem podstavy 20 cm a výškou 50 cm se rozvine do kruhového výseku. Jak velký je středový úhel tohoto výseku? - Povrch 32
Povrch rotačního kužele a obsah jeho podstavy jsou v poměru 18:5. Určete objem kužele, je-li jeho tělesná výška 12 cm.
- Bukový
Bukový školní model pravidelného čtyřbokého jehlanu má podstavou hranu dlouhou 20 cm a výšku 24 cm. Vypočítejte a) povrch jehlanu ve čtverečných decimetrech, b) hmotnost jehlanu v kilogramech, je-li hustota buku ρ=0,8g/cm³ - Střecha
Střecha domu má tvar pravidelného čtyřbokého jehlanu o výšce 5 m a hraně podstavy 7 m. Kolik je třeba tašek o obsahu 540 cm²? - Kolik Kolik m² měděného plechu třeba na výměnu střechy věže kuželovitého tvaru, jejíž průměr je 13 metrů a výška 24 metrů, pokud na zahnutí a odpad počítáme 8% materiálu?
- Plocha stanu
Vypočítejte, kolik plátna (bez podlahy) se spotřebuje na zhotovení stanu, který má tvar pravidelného čtyřbokého jehlanu. Hrana podstavy má délku 3 m a výška stanu je 2m. - Šikmo
Obrázek znázorňuje kužel se šikmou výškou (stranou) 10,5 cm. Zakřivená plocha kužele 115,5 cm². Vypočtěte na 3 platné číslice: * Poloměr základny * výšku * Objem kužele
Vypočítejte objem krychle, jejíž tělesová úhlopříčka má velikost 75 dm. Načrtněte si obrázek a tělesovou úhlopříčku barevně zvýrazněte.Máš úkol, nad kterým si lámeš alespoň 10 minut hlavu? Pošli nám úkol a my Ti ji zkusíme vypočítat. Řešení příkladů z matematiky.
