Objem + vyjádření neznámé ze vzorce - příklady a úlohy - strana 4 z 33
Počet nalezených příkladů: 653
- Povrch 32
Povrch rotačního kužele a obsah jeho podstavy jsou v poměru 18:5. Určete objem kužele, je-li jeho tělesná výška 12 cm. - Rovnostranného 81142
Rotační těleso vzniklo rotací rovnostranného trojúhelníku o délce strany a=2 cm kolem jedné z jeho stran. Vypočítejte objem tohoto rotačního tělesa. - Zubní pasta
Jak dlouhý bude váleček zubní pasty vytlačený z tuby, když je objem zubní pasty 100 ml a průměr otvoru 8 mm? - Kulová úseč 4
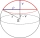Vypočítejte objem kulové úseče a povrch vrchlíku. Je-li poloměr koule r=5cm a poloměr kruhové podstavy úseče ρ=4cm.
- Podstavy
Podstavami pravidelného komolého čtyřbokého jehlanu jsou čtverce. Délky stran se liší o 6 dm. Tělesová výška je 7 dm. Objem tělesa je 1813 dm³. Vypočítejte délky hran obou podstav. - Krychli 4
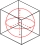Krychli o objemu 4096cm³ je opsána a vepsána koule. Vypočítejte, kolikrát je větší objem opsané koule než koule vepsané. - Objem 29
Objem kvádru je 3/25 m³. Plocha podstavy je 6/25 m². Jaká je jeho výška? - Obvod 34 Obvod podstavy pravidelného čtyřbokého jehlanu je stejně velký jako jeho výška. Jehlan má objem 288 dm³. Vypočítejte jeho povrch. Výsledek zaokrouhlete na celé dm².
- Malý Jirka
Malý Jirka chtěl vědět, kolik zubní pasty je v tubě a tak ji postupně všechnu vytlačil a v pokoji byl válec pasty. Dokážete odhadnout, jakou mohl mít délku? Počítejte pro hodnoty: vnitřní průměr hrdla pasty je 6 mm a objem pasty je 75 ml.
- Valec obecne
Jak vysoký je válec, jehož plášť má obsah rovný obsahu podstavy? Jaká je objem tohoto válce? - Pavel 8
Pavel má akvárium tvaru kvádru o objemu 240 litrů. Tomáš má akvárium, jehož všechny rozměry jsou polovina rozměrů Pavlova akvária. Jaký objem má Tomášovo akvárium? - Svislý
Svislý šestiboký hranol byl vytvořen opracováním krychle o hraně délky 8 cm. Podstava hranolu vznikne ze čtvercové stěny původní krychle oddělením 4 shodných pravoúhlých trojúhelníků s odvěsnami délek 3cm a 4cm. Výška hranolu je 8 cm. Jaký je objem šestib - Pro rozměry
Pro rozměry plaveckého bazénu platí: d : š : h = 10 : 4 : 1. Do bazénu se vejde 625 m³ vody. Vypočítejte, kolik m² obkladů je třeba zakoupit na obložení stěn bazénu, přidáme-li 5% na odpad. - Velikost 78514
Kvádr má délku 12cm, šířku 0,6dm. Výška má stejnou velikost jako hrana kostky, jejíž objem je 64cm³. Vypoctej objem kvádru v cm³.
- Kvádr 68
Kvádr má tělesovou úhlopříčku u=25 cm a strana b je oproti straně a o třetinu delší. Jaký je objem kvádru? - Pravoúhlého 75144
Poloměr pravoúhlého kruhového kužele je 9 cm a délka strany je 15 cm. Najděte na jedno desetinné místo: (i) Výši (ii) Objem kužele - Čtverečních 75014
Povrch krychle je roven 294 metrů čtverečních. Vypočtěte hranu a objem krychle. - Vyřízne kvádr
Z jednoho rohu původního kvádru se podle obrázku vyřízne kvádr o hloubce 4 cm, ale délce a šířce x cm (původní kvádr má rozměry 10x8x4 cm). Zbývající tvar má objem 199 cm³. Vypočítejte hodnotu x. - Krychlových 74674
Vypočítejte povrch a hranu krychle, pokud její objem se rovná 3375 metrů krychlových.
Dva podobné hrnce mají výšku 16 cm a 10 cm, pokud menší hrnec má objem 0,75l. Najděte objem většího hrnce.Máš úkol, nad kterým si lámeš alespoň 10 minut hlavu? Pošli nám úkol a my Ti ji zkusíme vypočítat. Řešení příkladů z matematiky.
