Komolý
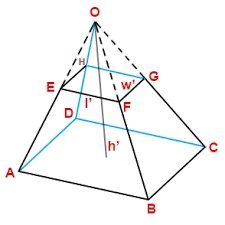
Komolý pravidelný čtyřboký jehlan má objem 74 cm3, výšku v = 6 cm a obsah dolní podstavy o 15 cm2 větší než obsah horní podstavy. Vypočítejte obsah horní podstavy.
Správná odpověď:
Tipy na související online kalkulačky
Hledáte pomoc s výpočtem kořenů kvadratické rovnice?
Máte soustavu rovnic a hledáte kalkulačku soustavy lineárních rovnic?
Tip: Převody jednotky objemu vám pomůže naše kalkulačka pro převody jednotek objemu.
Máte soustavu rovnic a hledáte kalkulačku soustavy lineárních rovnic?
Tip: Převody jednotky objemu vám pomůže naše kalkulačka pro převody jednotek objemu.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
- algebra
- kvadratická rovnice
- soustava rovnic
- vyjádření neznámé ze vzorce
- bikvadratická rovnice
- stereometrie
- jehlan
- komolý jehlan a kužel
- planimetrie
- obsah
Jednotky fyzikálních veličin:
Úroveň náročnosti úkolu:
Související a podobné příklady:
- Seříznutého 73454
Objem seříznutého kužele je V=38000π cm³. Poloměr dolní podstavy je o 10 cm větší, než poloměr horní podstavy. Určete poloměr podstav, pokud výška v=60 cm. - 4b jehlan 3
Pravidelný čtyrboký jehlan má obvod podstavy 44cm a tělesovou výšku 3,2dm. Vypočítejte jeho objem a povrch. - Je dán 21
Je dán pravidelný čtyřboký jehlan s délkou podstavné hrany a=15cm a výškou v=21cm. Rovnoběžně s podstavou vedeme dvě roviny tak, že rozdělil výšku jehlanu na tři stejné části. Vypočítej poměr objemů vzniklých 3 těles. - Máme pravidelný
Máme pravidelný čtyřboký jehlan s podstavnou hranou a=10 cm a výškou v=7cm. Vypočtěte 1/obsah podstavy 2/obsah pláště 3/povrch jehlanu 4/objem jehlanu
- Čtyřboký jehlan 9
Je dán pravidelný čtyřboký jehlan. Délka hrany podstavy a = 6,5 cm, boční hrana s = 7,5 cm. Vypočítejte objem a obsah pláště. - Pravidelný 9 Pravidelný čtyřboký jehlan má povrch 260 cm² a obsah jedné boční stěny 40 cm². Vypočítejte délku hrany podstavy a stěnovou výšku.
- Seříznutého 82013
Stínítko lampy jako komolý má výšku 12 cm a horní a dolní průměr 10 cm a 20 cm. Jaká plocha materiálů je potřebná k pokrytí zakřiveného povrchu seříznutého okraje?
