Z bodu 2
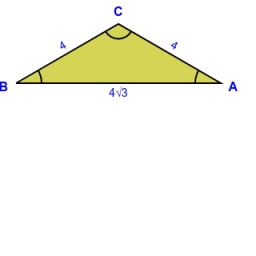
Z bodu na kružnici o průměru 8 cm jsou vedeny dvě shodné tětivy, které svírají úhel 60°. Vypočítej délku těchto tětiv.
Správná odpověď:
Zobrazuji 7 komentářů:
Žák
Hezký den,
pomůže mi někdo vysvětlit, na základě čeho je odvozen následující řádek ve výše uvedeném řešení. (r2 je r na druhou,t2 je t na druhou)
r2 = r2 + t2 - 2 . r . t . cos B
Tadeáš
pomůže mi někdo vysvětlit, na základě čeho je odvozen následující řádek ve výše uvedeném řešení. (r2 je r na druhou,t2 je t na druhou)
r2 = r2 + t2 - 2 . r . t . cos B
Tadeáš
Zs Ucitel
to je Kosinova veta pre trojuhelnik SSU ( znam 2 strany a uhel jedne prilehly). Vznikla kvadraticka rovnice se vydeli t ... vznikne linearni rovnice....
Žák
Děkuji za vysvětlení, tento příklad byl součástí testů v rámci přípravy na přijímací řízení na střední školy.
Sinovou a cosinovou větu se bohužel neučili. Pokud mám správné informace, tato látka se učí až na středních školách.
Sinovou a cosinovou větu se bohužel neučili. Pokud mám správné informace, tato látka se učí až na středních školách.
Zs Ucitel
Pak zkusime vysvetlit na zaklade uhlu 60 stupnu... bude tam rovnoramenny nebo rovnostranni trojuhelnik. Ale kdyby tam byl napr uhel 59 stupnu, pak asi kosinovu vetu treba vedet,,,,
Žák
Můžu poprosit o jaký rovnoramenný či rovnostranný trojúhelnik se jedná, a na základě čeho pak vypočítám délku jedné tětivy. Předem děkuji za odpověd.
Žák
Podařilo se mi vyřešit
Podařilo se mi najít řešení tohoto příkladu bez použití cosinové věty (což je učivo střední školy).
Snad je to správně.
V rovnostranné trojúhelníku ABC platí výška=těžnice a jednotlivé úhly měří všechny stejně 60°.
Pro výpočet použiji pravoúhlý trojúhelník SBSa a geometrickou funkci cos. Bod Sa je střed úsečky BC
v rovnostranném trojúhelníku ABC, úsečka SB je přeponou v pravoúhlém trojúhelníku SBSa a zároveň poloměrem (4 cm) pro kružnici opsanou v rovnostranném trojúhelníku ABC.
cos 30° = b : c (přepona c je poloměr opsané kružnice 4 cm, odvěsna b je polovina délky tětivy).
cos 30° = b : 4
0.866 = b : 4
b = 3.46 cm
celá tětiva 3.46 x 2 = 6.92 cm
Délka jedné tětivy se rovná 6,92cm.
Podařilo se mi najít řešení tohoto příkladu bez použití cosinové věty (což je učivo střední školy).
Snad je to správně.
V rovnostranné trojúhelníku ABC platí výška=těžnice a jednotlivé úhly měří všechny stejně 60°.
Pro výpočet použiji pravoúhlý trojúhelník SBSa a geometrickou funkci cos. Bod Sa je střed úsečky BC
v rovnostranném trojúhelníku ABC, úsečka SB je přeponou v pravoúhlém trojúhelníku SBSa a zároveň poloměrem (4 cm) pro kružnici opsanou v rovnostranném trojúhelníku ABC.
cos 30° = b : c (přepona c je poloměr opsané kružnice 4 cm, odvěsna b je polovina délky tětivy).
cos 30° = b : 4
0.866 = b : 4
b = 3.46 cm
celá tětiva 3.46 x 2 = 6.92 cm
Délka jedné tětivy se rovná 6,92cm.
Tipy na související online kalkulačky
Hledáte pomoc s výpočtem kořenů kvadratické rovnice?
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Kosinovú větu přímo používá kalkulačka SUS trojúhelníku.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Kosinovú větu přímo používá kalkulačka SUS trojúhelníku.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
- algebra
- kvadratická rovnice
- vyjádření neznámé ze vzorce
- planimetrie
- pravoúhlý trojúhelník
- kruh, kružnice
- trojúhelník
- kosinová věta
- tětiva
- goniometrie a trigonometrie
- sinus
- kosinus
Jednotky fyzikálních veličin:
Úroveň náročnosti úkolu:
Související a podobné příklady:
- Rovnoběžné tětivy
 V kružnici s průměrem 70 cm jsou narýsované dvě rovnoběžné tětivy tak, že střed kružnice leží mezi tětivami. Vypočítejte vzdálenost těchto tětiv, pokud jedna z nich má délku 42 cm a druhá 56 cm.
V kružnici s průměrem 70 cm jsou narýsované dvě rovnoběžné tětivy tak, že střed kružnice leží mezi tětivami. Vypočítejte vzdálenost těchto tětiv, pokud jedna z nich má délku 42 cm a druhá 56 cm. - Kružnice
 V kružnici s poloměrem 7,5 cm jsou sestrojeny 2 rovnoběžné tětivy, jejichž délky jsou 9 cm a 12 cm. Vypočítejte vzdálenost těchto tětiv (pokud jsou možné dvě řešení napište obě).
V kružnici s poloměrem 7,5 cm jsou sestrojeny 2 rovnoběžné tětivy, jejichž délky jsou 9 cm a 12 cm. Vypočítejte vzdálenost těchto tětiv (pokud jsou možné dvě řešení napište obě). - Dvě tětivy
 V kružnici jsou vedeny dvě tětivy dlouhé 30 a 34 cm. Kratší z nich je od středu dvakrát dál než delší. Urči poloměr kružnice.
V kružnici jsou vedeny dvě tětivy dlouhé 30 a 34 cm. Kratší z nich je od středu dvakrát dál než delší. Urči poloměr kružnice. - V kružnici
 V kružnici o poloměru 8,5 cm jsou sestrojeny dvě rovnoběžné tětivy, jejichž délky jsou 9 cm a 12 cm. Vypočítejte vzdálenost tětiv v kružnici.
V kružnici o poloměru 8,5 cm jsou sestrojeny dvě rovnoběžné tětivy, jejichž délky jsou 9 cm a 12 cm. Vypočítejte vzdálenost tětiv v kružnici.
- Rovnoběžné tětivy
 V kružnici s r = 26 cm jsou narýsované 2 rovnoběžné tětivy. Jedna tětiva má délku t1 = 48 cm a druhá má délku t2 = 20cm, přičemž střed leží mezi nimi. Vypočítejte vzdálenost dvou tětiv.
V kružnici s r = 26 cm jsou narýsované 2 rovnoběžné tětivy. Jedna tětiva má délku t1 = 48 cm a druhá má délku t2 = 20cm, přičemž střed leží mezi nimi. Vypočítejte vzdálenost dvou tětiv. - Dvě tětivy
 Je dána kružnice k (S, r). Z bodu A který patří k jdou dvě tětivy s délkou r. Jaký úhel svírají? Narysuj a odměř.
Je dána kružnice k (S, r). Z bodu A který patří k jdou dvě tětivy s délkou r. Jaký úhel svírají? Narysuj a odměř. - Vypočítejte 7214
 Ke kružnici o poloměru 76 mm jsou z bodu C vedeny dvě tečny. Vzdálenost obou dotykových bodů je 14 mm. Vypočítejte vzdálenost bodu C od středu kružnice.
Ke kružnici o poloměru 76 mm jsou z bodu C vedeny dvě tečny. Vzdálenost obou dotykových bodů je 14 mm. Vypočítejte vzdálenost bodu C od středu kružnice.
