Sousedních 16793
Všechny boční hrany čtyřboké pyramidy ABCDV jsou stejně dlouhé a její základna je obdélník. Určete jeho objem, pokud znáte odchylky rovin sousedních bočních stěn a roviny základny a výšku h pyramidy.
Správná odpověď:
Tipy na související online kalkulačky
Tip: Převody jednotky objemu vám pomůže naše kalkulačka pro převody jednotek objemu.
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
- algebra
- vyjádření neznámé ze vzorce
- stereometrie
- jehlan
- planimetrie
- pravoúhlý trojúhelník
- trojúhelník
- čtverec
- goniometrie a trigonometrie
- tangens
- kotangens
Jednotky fyzikálních veličin:
Úroveň náročnosti úkolu:
Související a podobné příklady:
- Průsečík přímky a roviny
Je dán pravidelný čtyřboký jehlan ABCDV, uvnitř jeho hrany AV je bod M, na prosloužené úsečce DC za bod C je bod N. Sestrojte průsečnici roviny MNV s rovinou BCV a průsečík přímky MN a roviny BCV. - Vypočtěte 10
Vypočtěte velikost odchylky tělesové úhlopřičky a boční hrany c kvádru o rozměrech: a=28cm, b=45cm a c=73cm. Dále vypočtěte velikost odchylky tělesové úhlopřičky od roviny podstavy. - Roviny bočních stěn
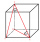Vypočítej objem a povrch kvádru jehož strana c má délku 30 cm a tělesová úhlopříčka svírá s rovinami bočních stěn úhly o velikostech 24 st. 20’, 45 st. 30’ - Lichoběžník - zahrada
Na zahradě tvaru lichoběžníku, který má základny dlouhé 30 m a 20 m a výšku dlouhou 20 m, napršelo 10 mm vody. Kolik kbelíků vody bychom potřebovali na stejně vydatné polití zahrady, pokud má kbelík objem 15 l?
- Pravidelný 8
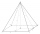Pravidelný čtyřboký jehlan má podstavnou hranu a=1,56 dm a výšku v= 2,05dm. Vypočtěte : a) odchylku roviny boční stěny od roviny podstavy b) odchylku boční hrany od roviny podstavy - Je dán 21
Je dán pravidelný čtyřboký jehlan s délkou podstavné hrany a=15cm a výškou v=21cm. Rovnoběžně s podstavou vedeme dvě roviny tak, že rozdělil výšku jehlanu na tři stejné části. Vypočítej poměr objemů vzniklých 3 těles. - Řezy kužele
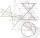Kužel s poloměrem podstavy 11 cm a výškou 11 cm rozdělíme rovinami rovnoběžnými s podstavou na tři tělesa. Roviny rozdělí výšku kužele na tři stejné části. Určete poměr objemů největšího a nejmenšího vzniklého tělesa.
