Podobnost trojúhelníků - příklady - strana 6 z 8
Počet nalezených příkladů: 155
- MO Z9–I–2 - 2017
V lichoběžníku VODY je VO delší základnou a průsečík úhlopříček K dělí úsečku VD v poměru 3:2 . Obsah trojúhelníku KOV je 13,5 cm². Urči obsah celého lichoběžníku. - Garáž 2
V garáži stojí u stěn naproti sobě dvě latě: jedna 2 metry dlouhá a druhá 3 metry dlouhá. Spadnou proti sobě a opřou se o protilehlé stěny garáže obě latě se překříží ve výšce 70 cm nad podlahou garáže. Jak široká je garáž? - Vzdálenosti 5148
Ve vzdálenosti 10 m od břehu řeky naměřili základnu AB = 50 m rovnoběžně s břehem. Bod C na druhém břehu řeky je vidět z bodu A pod úhlem 32°30' az bodu B pod úhlem 42°15'. Vypočítejte šířku řeky. - Zrcátko
Jak daleko od svých nohou musel Pavel umístit zrcátko, aby v něm uviděl vrchol věže vysoké 12 m? Výška Pavlových očí očí nad vodorovnou rovinou je 160 cm, Pavel je od věže vzdálen 20 m.
- Koeficient podobnosti
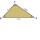Trojúhelníky ABC a A "B" C "jsou podobné koeficientem podobnosti 2. Velikosti úhlů trojúhelníku ABC jsou α = 35° a β = 48°. Urči velikosti všech úhlů trojúhelníku A" B "C". - Vitrínka
Do skříňky třeba umístit skleněnou poličku ve výšce 1m od spodku vitríny. Jak velkou polici do ní v této výši umístíme? Vitrínka je pravoúhlý trojúhelník s odvěsnami 2 m a 2,5 m. - Thalés
Thalés je vzdálený 1 m od jámy. Oči má ve výšce 150 cm nad zemí a dívá do jámy s průměrem 120 cm podle obrázku. Vypočítejte hloubku jámy. - Komolý jehlan
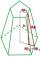Vypočtěte objem pravidelného šestibokého komolého jehlanu, jestliže je délka hrany dolní podstavy 30 cm, horní podstavy 12 cm a pokud délka boční hrany je 41 cm. - Podobnost 7
Zjisti, zda trojúhelníky ABC a A´B´C´jsou podobné, urči koeficient podobnosti a podobnost zapiš: a=40 mm, b=48 mm, c=32 mm a´=60 mm, b´=50 mm, c´=40 mm
- Podobný trojúhelník
Strany trojúhelníku ABC mají délky 4 cm,5 cm a 7 cm. Sestroj trojúhelník A´B´C´ podobný trojúhelníku ABC, který má obvod 12 cm. - Klínový řemen
Vypočítejte délku klínového řemene pokud průměr řemenic je: d1 = 600mm d2 = 120mm d = 480mm (vzdálenost os řemenic) - Stín stromu
Stín stromu je dlouhý 16m. Stín vedle něj stojící 2m vysoké turistické značky je tehdy dlouhý 3,2 m. Jakou výšku v metrech má strom? - Sluneční paprsky
Dopadají-li sluneční paprsky pod úhlem 60°, vrhá slavná egyptská Cheopsova pyramida, která je dnes vysoká 137,3m, stín dlouhý 79,3m. Vypočítejte dnešní výšku sousední Chefrenovi pyramidy, jejíž stín měří v témže okamžiku 78,8 m, a dnešní výšku nedaleké Mi - Pravítko
Ako daleko od Petra stojí dvoumetrový Jirka? Petr se na Jirku dívá přes pravítko, které drží v natažené ruce 60 cm od oka a na pravítku změřil Jirkovu výšku na 15 mm.
- Strom
Strom kolmý k vodorovnému povrchu vrhá stín 8,32 m. Současně metrová tyč kolmá k vodorovnému povrchu má délku stínu 64 cm. Jak je vysoký strom? - Podobnosť trojuholníkov
a= 6cm, b=8cm, c=? , a'=? , b'=12cm, c'=15cm - Úhly2
Určete velikost nejmenšího vnitřního úhlu pravoúhlého trojúhelníku, jehož velikosti stran tvoří po sobě jdoucí členy aritmetické posloupnosti. - Maják
Muž, 180 cm vysoký, kráčí po nábřeží přímo k majáku. Mužův stín, způsobený světlem majáku, je na začátku dlouhý 5,4 m. Když se muž přiblíží k majáku o 90 metrů, zkrátí se jeho stín o 3 metry. Jak vysoký je maják a jak daleko je muž od něho vzdálený? - Strany z poměru
Vypočítej obvod trojúhelníka s obsahem 84 cm² platí-li a:b:c = 10:17:21
Vypočítejte strany pravoúhlého trojúhelníku pokud odvěsna a = 6cm a úsek na přepony, který je přilehlý k druhé odvěsně Cb je 5cm.Máš úkol, nad kterým si lámeš alespoň 10 minut hlavu? Pošli nám úkol a my Ti ji zkusíme vypočítat. Řešení příkladů z matematiky.
