Šířka řeky
Ve vzdálenosti 10 m od břehu řeky naměřili základnu AB = 50 m rovnoběžně s břehem. Bod C na druhém břehu řeky je vidět z bodu A pod úhlem 32°30' a z bodu B pod úhlem 42°15'. Vypočítejte šířku řeky.
Vaše odpověď:
Vaše odpověď:
Tipy na související online kalkulačky
Máte soustavu rovnic a hledáte kalkulačku soustavy lineárních rovnic?
Chcete proměnit jednotku délky?
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte si převody jednotek úhlů úhlové stupně, minuty, sekundy, radiány.
Chcete proměnit jednotku délky?
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte si převody jednotek úhlů úhlové stupně, minuty, sekundy, radiány.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
geometriealgebraplanimetriegoniometrie a trigonometrieJednotky fyzikálních veličinÚroveň náročnosti úkolu
Související a podobné příklady:
- Budova 3
Budova vysoká 15 m je vzdálená od břehu řeky 30 m. Ze střechy této budovy je vidět šířku řeky pod úhlem 15°. Jak je řeka široká? - Strom a řeka
Strom, který je na protějším břehu řeky vidíme pod úhlem 15° ze vzdálenosti 41 m od břehu řeky. Ze břehu řeky vidíme pod úhlem 31°. Jak vysoký je strom? - Vzdálenosti - majáky
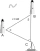Dva majáky A, B spatřily loď, jak je znázorněno na obrázku. Jaká je vzdálenost mezi lodí a majákem A s přesností na jednu desetinu námořní míle? Obrázek - vzdálenost mezi majáky A a B je 40 námořních mil. Z bodu A je vidět úhel pohledu 57° a z bodu B pod - Komín
Ze vzdálenosti 36 metrů od paty komína je vidět jeho vršek pod uhlem 53°. Vypočítej výšku komína. Zaokrouhli na dm. - Výška domu
Z vyhlídky na kostelní věži ve výšce 65 m je vidět vrchol domu pod hloubkovým úhlem alfa = 45° a jeho spodek pod hloubkovým úhlem beta = 58°. Vypočtěte výšku domu a jeho vzdálenost od kostela. - Řeka
Z pozorovatelny 20 m vysoké a vzdálené 40 m od břehu řeky se jeví šířka řeky v zorném úhlu φ=18°. Vypočítejte šířku řeky. - Z rozhledně
Z rozhledně vysoké 40 m je vidět vrchol topolu pod hloubkovym uhlem o velikosti 50°10' a patu topolu v hloubkovem úhlu o velikosti 58°. Vypocitejte výšku topolu.
