Analytická geometrie - příklady - strana 4 z 13
Počet nalezených příkladů: 242
- Je dán 13
 Je dán pravidelný čtyřboký hranol ABCDEFGH s podstavnou hranou AB délky 8 cm a výškou 6 cm. Bod M je střed hrany AE. Určete vzdálenost bodu M od roviny BDH.
Je dán pravidelný čtyřboký hranol ABCDEFGH s podstavnou hranou AB délky 8 cm a výškou 6 cm. Bod M je střed hrany AE. Určete vzdálenost bodu M od roviny BDH. - Lichoběžníku 44431
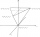
 1. V kartézském rámci o funkcích f a g víme, že: funkce (f) je definována vztahem f (x) = 2x², funkce (g) je definována vztahem g (x) = x + 3, bod (O) je počátkem reference, bod (C) je průsečík grafu funkce (g) s osou pořadnice, body A a B jsou průsečíky
1. V kartézském rámci o funkcích f a g víme, že: funkce (f) je definována vztahem f (x) = 2x², funkce (g) je definována vztahem g (x) = x + 3, bod (O) je počátkem reference, bod (C) je průsečík grafu funkce (g) s osou pořadnice, body A a B jsou průsečíky - Těžiště tetraeder
 Určete polohu těžiště soustavy čtyř hmotných bodů, které mají hmotnosti, m1, m2 = 2m1, m3 = 3M1 a m4 = 4m1, pokud leží ve vrcholech rovnoramenné tetraedru. (Ve všech případech mezi sousedními hmotnými body je vz
Určete polohu těžiště soustavy čtyř hmotných bodů, které mají hmotnosti, m1, m2 = 2m1, m3 = 3M1 a m4 = 4m1, pokud leží ve vrcholech rovnoramenné tetraedru. (Ve všech případech mezi sousedními hmotnými body je vz - Kružnicemi 44221
 Pro kružnice k1 (S1,4cm) a k2(S2,3cm) a platí že |S1S2| = 8cm. Určete vzdálenost mezi kružnicemi K1 a K2.
Pro kružnice k1 (S1,4cm) a k2(S2,3cm) a platí že |S1S2| = 8cm. Určete vzdálenost mezi kružnicemi K1 a K2.
- Rovnoběžníku 40421
 Je-li ∠BAD mezi stranami AB a AD rovnoběžníku θ, co je pak tan θ? Viz diagram: A=(7,1) B=(5,-2) C=(12,1) D=(14,4)
Je-li ∠BAD mezi stranami AB a AD rovnoběžníku θ, co je pak tan θ? Viz diagram: A=(7,1) B=(5,-2) C=(12,1) D=(14,4) - Parametrické vyjádření
 Bod A [6; -2]. Bod B = [-3; 1] Zapiš parametrické vyjádření úsečky BA tak, aby t patřilo do uzavřený interval < 0;3 >
Bod A [6; -2]. Bod B = [-3; 1] Zapiš parametrické vyjádření úsečky BA tak, aby t patřilo do uzavřený interval < 0;3 > - Vzdáleností 36831
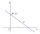 Je dána přímka p a dva vnitřní body jedné z polorovin, určených přímkou p. Najdi na přímce p bod X tak, aby součet jeho vzdáleností od bodů A, B byl nejmenší.
Je dána přímka p a dva vnitřní body jedné z polorovin, určených přímkou p. Najdi na přímce p bod X tak, aby součet jeho vzdáleností od bodů A, B byl nejmenší. - Čtyřúhelník
 Urč o jaký čtyřúhelník ABCD jde a vypočítej jeho obvod A/2,4/, B/-2,1/, C/-2,-2/, D/2,-5/. A. Útvar je: B. Jeho obvod měří:
Urč o jaký čtyřúhelník ABCD jde a vypočítej jeho obvod A/2,4/, B/-2,1/, C/-2,-2/, D/2,-5/. A. Útvar je: B. Jeho obvod měří: - Souřadnice 36751
 Vypočítej délku kružnice a urč souřadnice středu kružnice když je dán její průměr XY, X /-3,2/a Y /-3, -4/.
Vypočítej délku kružnice a urč souřadnice středu kružnice když je dán její průměr XY, X /-3,2/a Y /-3, -4/.
- Geometrický 34741
 Jaký geometrický útvar vytvářejí všechny body v rovině, které mají od daného bodu v rovině stejnou vzdálenost?
Jaký geometrický útvar vytvářejí všechny body v rovině, které mají od daného bodu v rovině stejnou vzdálenost? - Kolmý průmět
 Určete vzdálenost bodu B [1, -3] od kolmého průmětu bodu A [3, -2] na přímku 2 x + y + 1 = 0.
Určete vzdálenost bodu B [1, -3] od kolmého průmětu bodu A [3, -2] na přímku 2 x + y + 1 = 0. - Souřadnice vrcholů
 Jsou dány souřadnice vrcholů trojúhelníku: P (-12,6), Q (4,0), R (-8, -6). Načrtněte obrázek trojúhelníku. Najděte obsah trojúhelníku.
Jsou dány souřadnice vrcholů trojúhelníku: P (-12,6), Q (4,0), R (-8, -6). Načrtněte obrázek trojúhelníku. Najděte obsah trojúhelníku. - Z bodu 3
 Z bodu A ve výšce 2m a z bodu B ve výšce 6m jsou současně vrženy proti sobě dvě tělesa. První z bodu A s horizontální rychlostí 8m/s a druhé směrem dolů pod úhlem 45 stupňů k horizontále s takovou počáteční rychlostí, aby se tělesa podobu letu srazila. Ho
Z bodu A ve výšce 2m a z bodu B ve výšce 6m jsou současně vrženy proti sobě dvě tělesa. První z bodu A s horizontální rychlostí 8m/s a druhé směrem dolů pod úhlem 45 stupňů k horizontále s takovou počáteční rychlostí, aby se tělesa podobu letu srazila. Ho - Přímka 6
 Přímka p je dána bodem P [ - 0,5;1] a směrovým vektorem s= (1,5; - 3) určete: A) hodnotu parametru t pro body X [ - 1,5;3], Y [1; - 2] přímky p B) zda body R [0,5; - 1], S [1,5;3] leží na přímce p C) parametrické rovnice přímky m || p, prochází-li přímka
Přímka p je dána bodem P [ - 0,5;1] a směrovým vektorem s= (1,5; - 3) určete: A) hodnotu parametru t pro body X [ - 1,5;3], Y [1; - 2] přímky p B) zda body R [0,5; - 1], S [1,5;3] leží na přímce p C) parametrické rovnice přímky m || p, prochází-li přímka
- Umístěte vektor
 Vektor AB, jestliže A (3, -1), B (5,3) umístěte do bodu C (1,3) tak že, AB = CO
Vektor AB, jestliže A (3, -1), B (5,3) umístěte do bodu C (1,3) tak že, AB = CO - Rostoucí funcke
 Která z funkci je rostoucí? a) y = 2-x b) y = 20 c) y = (x + 2). (-5) d) y = x-2
Která z funkci je rostoucí? a) y = 2-x b) y = 20 c) y = (x + 2). (-5) d) y = x-2 - Trojúhelník 32183
 V rovině je dán trojúhelník ABC. A(-3,5), B(2,3), C(-1,-2) zapište souřadnice vektorů u, v, w pokud u=AB, v=AC, w=BC. Zapište souřadnice středů úseček SAB(. .), SAC(. .. ), SBC(. .. )
V rovině je dán trojúhelník ABC. A(-3,5), B(2,3), C(-1,-2) zapište souřadnice vektorů u, v, w pokud u=AB, v=AC, w=BC. Zapište souřadnice středů úseček SAB(. .), SAC(. .. ), SBC(. .. ) - Obecná rovnice
 Ve všech příkladech napište OBECNOU ROVNICI přímky, která je nějakým způsobem zadána. A)přímka je dána parametricky: x = - 4 + 2p;y = 2 - 3p B) přímka je dána směrnicově: y = 3x - 1 C) přímka je dána dvěma body: A [3; -3], B [-5; 2] D) přímka protíná
Ve všech příkladech napište OBECNOU ROVNICI přímky, která je nějakým způsobem zadána. A)přímka je dána parametricky: x = - 4 + 2p;y = 2 - 3p B) přímka je dána směrnicově: y = 3x - 1 C) přímka je dána dvěma body: A [3; -3], B [-5; 2] D) přímka protíná - Dotyčnica elipsy
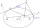 Najděte dotyčnici elipsy 9 x² + 16 y² = 144, která má sklon k = -1
Najděte dotyčnici elipsy 9 x² + 16 y² = 144, která má sklon k = -1
Máš úkol, nad kterým si lámeš alespoň 10 minut hlavu? Pošli nám úkol a my Ti ji zkusíme vypočítat. Řešení příkladů z matematiky.
