Z9–I–1
Vo všetkých deviatich poliach obrazca majú byť vyplnené prirodzené čísla tak, aby platilo:
• každé z čísel 2, 4, 6 a 8 je použité aspoň raz,
• štyri z polí vnútorného štvorca obsahujú súčiny čísel zo susediacich polí vonkajšieho štvorca,
• v kruhu je súčet čísel zo susedných polí vnútorného štvorca.
Zistite, ktoré najmenšie a ktoré najväčšie číslo môže byť napísané v kruhu.
• každé z čísel 2, 4, 6 a 8 je použité aspoň raz,
• štyri z polí vnútorného štvorca obsahujú súčiny čísel zo susediacich polí vonkajšieho štvorca,
• v kruhu je súčet čísel zo susedných polí vnútorného štvorca.
Zistite, ktoré najmenšie a ktoré najväčšie číslo môže byť napísané v kruhu.
Správna odpoveď:
Zobrazujem 4 komentáre:
Žiak
Jaká je odpověď nebo postup počítám matematickou olympiádou a nevychází mi to , tady ale také není výsledek ????
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Súvisiace a podobné príklady:
- Adam MO (asi MO Z8)
Adam napísal nasledujúci súčet s piatimi tajnými sčítancami: a + bb + ccc + dddd + eeeee. Prezradil, že znaky „a, b, c, d, e“ predstavujú navzájom rôzne cifry 1, 2, 3, 4, 5 a že výsledný súčet je deliteľný 11. Ktoré najmenšie a ktoré najväčšie číslo môž - Šesťmiestne 84145
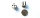Pepina hádzala hracou kockou. Prvé číslo, ktoré jej padlo, napísala na papier, druhé napísala vpravo vedľa prvého, tretie napísala vpravo vedľa druhého atď., až po šiestom hode mala napísané šesťmiestne číslo. a) Aké najmenšie číslo deliteľné dvoma mohla - MO Z6-6-1
Do prázdnych polí v nasledujúcom obrázku doplňte celé čísla väčšie ako 1 tak, aby v každom tmavšom políčku bol súčin čísel zo susedných svetlejších políčok: Aké je číslo je v strede? - Dve číslice
Z čísla 547 191 807 vyškrtnite 2 číslice, tak aby ste dostali čo najmenšie číslo deliteľné 5. Napíšte súčet vyškrtnutých čísel
- Osemsten súčet
Na každej stene pravidelného osemstenu je napísané jedno z čísel 1, 2, 3, 4, 5, 6, 7 a 8, pričom na rôznych stenách sú rôzne čísla. Pri každej steny Janko určil súčet čísla na nej napísaného s číslami troch susedných stien. Takto dostal osem súčtov, ktoré - Určte 13
Určte počet všetkých štvorciferných prirodzených čísel, v dekadickom zápise, v ktorých nie je číslica 0 a zo zvyšných deviatich čísel sa v ňom každá nachádza najviac raz. - MO Z8–I–3 - 2017 - Adelka
Adelka mala na papieri napísané dve čísla. Keď k nim pripísala ešte ich najväčší spoločný deliteľ a najmenší spoločný násobok, dostala štyri rôzne čísla menšie ako 100. S úžasom zistila, že keď vydelí najväčšie z týchto štyroch čísel najmenším, dostane na
