Povrch tělesa + Pythagorova věta - příklady a úlohy - poslední strana
Počet nalezených příkladů: 298
- Stěnová úhlopříčka
Vypočítejte délku stěnové úhlopříčky krychle, jejíž povrch se rovná 384 centimetrů čtverečních. - Hranol 8
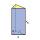Urč objem a povrch hranolu s podstavou rovnostranného trojúhelníku pokud strana a je 7 dm a výška tělesa 1,5 m - Rovnostranný 2714
Urč objem a povrch trojbokého hranolu o výšce 9 cm pokud podstava je rovnostranný trojúhelník se stranou 8 cm. - Vypočítejte
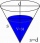Vypočítejte objem a povrch kužele, jehož osový řez je rovnostranný trojúhelník s délkou strany a = 18cm.
- Koule a krychle
Kolik % povrchu koule o poloměru 12cm tvoří povrch krychle vepsané do této koule? - Krychle z koule
Jaký největší povrch (v cm²) může mít krychle, která se vyřízne z koule o poloměru 43 cm? - Čtvercovou 46151
Vypočítej povrch jehlanu se čtvercovou podstavou o hraně délky 6cm a výšce 6cm. - Vypočtěte 17
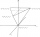Vypočtěte povrch pravidelného čtyřstěnu, je-li délka stěnové výšky Vs=1 dm - Kužel
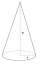Vypočtěte objem a povrch kužele, jestliže jeho poloměr r = 6 cm a strana s = 10 cm.
- Vypočítejte 31
Vypočítejte povrch, objem a délku tělesové úhlopříčky krychle o hraně délky 4 dm. - Krychle - stěna
V krychle ABCDEFGH je |CF|=4 √ 2. Jaký je povrch krychle? - Povrch kužele
Vypočítejte povrch kužele, když znáte průmer podstavy 25cm a vyšku 40 cm. - Vypočítejte 6580
Rotační kužel má výšku 20 cm a poloměr 18 cm. Vypočítejte jeho povrch. - Obdélníkovou 46201
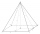Vypočítej povrch jehlanu s obdélníkovou podstavou o rozměrech 9cm a 4cm a výšce 6cm.
- Krychle 3
Urči povrch krychle, má - li její tělesová úhlopříčka velikost 6 cm. - Vypočítejte 11
Vypočítejte povrch S a objem V pravidelného čtyřbokého jehlanu se stranou podstavy a=5 m a tělesovou výškou 14 m. - Vypočítejte 82152
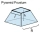Seříznutý jehlan se skládá ze čtvercové základny o délce 10 cm a vrchního čtverce o délce 7 cm. Výška seříznutého jehlanu je 6 cm. Vypočítejte povrch a objem. - Seříznutého 82013
Stínítko lampy jako komolý má výšku 12 cm a horní a dolní průměr 10 cm a 20 cm. Jaká plocha materiálů je potřebná k pokrytí zakřiveného povrchu seříznutého okraje?
Máš úkol, nad kterým si lámeš alespoň 10 minut hlavu? Pošli nám úkol a my Ti ji zkusíme vypočítat. Řešení příkladů z matematiky.
