Příklady na obsah pravoúhlého trojúhelníku - strana 21 z 28
Počet nalezených příkladů: 556
- Pravidelného 83324
Objem pravidelného čtyřbokého jehlanu je 72 cm³. Jeho výška se rovná délce podstavné hrany. Vypočítej délku podstavné a povrch jehlanu. - Svislý
Svislý šestiboký hranol byl vytvořen opracováním krychle o hraně délky 8 cm. Podstava hranolu vznikne ze čtvercové stěny původní krychle oddělením 4 shodných pravoúhlých trojúhelníků s odvěsnami délek 3cm a 4cm. Výška hranolu je 8 cm. Jaký je objem šestib - Komolý jehlan 4
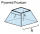Betonový podstavec tvaru pravidelného čtyřbokého komolého jehlanu má výšku 12 cm, hrany podstavy mají délky 2,4 a 1,6 dm. Vypočítej povrch podstavce. - Trojboký hranol
Podstava kolmého trojbokého hranolu je pravoúhlý trojúhelník, jehož přepona je 10cm a jedna odvěsna 8cm. Výška hranolu je 75% z obvodu podstavy. Vypočtěte objem a povrch hranolu.
- Střecha
1/2 plochy střechy ve tvaru pravidelného čtyřbokého jehlanu s hranou podstavy 7 m a výškou 5 m je už pokryta krytinou. Kolik třeba ještě pokrýt? - Slunečník
Slunečník má tvar pláště šestibokého pravidelného jehlanu, jehož podstavná hrana a=6dm a výška v=25cm. Kolik látky je třeba na zhotovení slunečníku, počítáme-li na spoje a odpad 10%. - Plášť 8
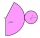Plášť kužele je vytvořen svinutím kruhové úseče o poloměru 1. Pro jaký středový úhel dané kruhové výseče bude objem vzniklého kužele maximální? - Správce hradu
Správce hradu se pokouší odhadnout, kolik čtverečných metrů plechu bude přibližně třeba na novou střechu věže. Střecha má tvar kužele. Správce hradu ví, že průměr věže je 4,6 metru a výška je 5,2 metru. Kolik čtverečných metrů střecha měří? - Nádrž
Nádrž má tvar pravidelného osmibokého hranolu bez horní podstavy. Podstavná hrana má a = 3m, boční hrana b = 6m. Kolik plechu třeba na zhotovení nádrže? Neberte v úvahu ztráty, ani tloušťku plechu.
- Podstava
Podstavou kvádru je obdélník se stranou 7,5 cm a úhlopříčkou 12,5 cm. Objem kvádru je V = 0,9 dm³. Vypočtěte povrch kvádru. - Trojboký hranol
Rovina, která prochází hranou AB a středem hrany CC' pravidelného trojbokého hranolu ABCA'B'C', svírá s podstavou úhel 46 stupňů, |AB| = 12 cm. Vypočítejte objem hranolu. - Rotační kužel
Objem rotačního kužele je 733 cm³ a strana kužele svírá s rovinou podstavy úhel 75°. Vypočítejte obsah pláště rotačního kužele. - Zaplatíme 33361
Střecha hradní věže má tvar kužele o průměru podstavy 12 m a výšce 8m. Kolik eur zaplatíme za pokrytí střechy, pokud 1m čtvereční krytiny stojí 3,5 eura? - Pravidelného 6610
Plášť rotačního válce je 4krát větší než obsah jeho podstavy. Určete objem pravidelného trojbokého hranolu, který je ve válci vepsán. Poloměr podstavy válce je 10 cm.
- Střecha
Střecha domu má tvar pravidelného čtyřbokého jehlanu o výšce 5 m a hraně podstavy 7 m. Kolik je třeba tašek o obsahu 540 cm²? - Plocha stanu
Vypočítejte, kolik plátna (bez podlahy) se spotřebuje na zhotovení stanu, který má tvar pravidelného čtyřbokého jehlanu. Hrana podstavy má délku 3 m a výška stanu je 2m. - Stínidlo
Stínidlo ve tvaru kužele má průměr 30 cm a výšku 10 cm. Kolik cm² materiálu budeme potřebovat, počítáme-li 10% na odpad? - 4-boký jehlan v1
Vypočítej objem a povrch pravidelného 4bokého jehlanu, jehož podstavna hrana je 4 cm. Odchylka bočni steny od roviny je 60 stupňů. - Střecha domu
Střecha domu má tvar pravidelného čtyřbokého jehlanu s podstavnou hranou 16 m. Kolik m² je třeba na její pokrytí, jestliže sklon střechy 45° a na spoje a odpad počítáme 8% plechu navíc?
Rozhledna je kryta střechou tvaru pravidelného čtyřbokého jehlanu s podstavnou hranou 8 m a výškou 6 m. 60% krytiny je třeba vyměnit. Kolik m² je třeba zakoupit?Máš úkol, nad kterým si lámeš alespoň 10 minut hlavu? Pošli nám úkol a my Ti ji zkusíme vypočítat. Řešení příkladů z matematiky.
