Pythagorean theorem - practice problems - page 2 of 70
A common proof of the Pythagorean Theorem is called the "area proof". To prove the theorem using this method, we can create a square with side length c and two smaller squares with side lengths a and b, as shown in the figure. We can then place the smaller squares next to each other to form a rectangle with area a x b. We can then see that the area of the square with side length c is equal to the sum of the areas of the smaller squares, which is equal to the area of the rectangle. This demonstrates that c2 = a2 + b2, as stated in the theorem.Another proof is Euclidean proof which is based on the Euclidean geometry and construction of a line segment that is c and perpendicular to the line segment of a and b.
Number of problems found: 1397
- Three 235
 Three houses form a triangular shape. House A is 50 feet from house C and house B is 60 feet from house C. The measure is angle ABC is 80 degrees. Draw a picture and find the distance between A and B.
Three houses form a triangular shape. House A is 50 feet from house C and house B is 60 feet from house C. The measure is angle ABC is 80 degrees. Draw a picture and find the distance between A and B. - General right triangle
 In a right triangle, if a =x+34 and b = x and c= 50, then solve for x. Side c is a hypotenuse. Then discuss the case when a or b is a hypotenuse.
In a right triangle, if a =x+34 and b = x and c= 50, then solve for x. Side c is a hypotenuse. Then discuss the case when a or b is a hypotenuse. - South and then east
 William walks 16 m south from his house and turns east to walk 63 m to reach his friend's house. While returning, he walks diagonally from his friend's house to reach back to his house. What distance did he walk while returning?
William walks 16 m south from his house and turns east to walk 63 m to reach his friend's house. While returning, he walks diagonally from his friend's house to reach back to his house. What distance did he walk while returning? - An isosceles triangle
 An altitude is drawn from the vertex of an isosceles triangle, forming a right angle and two congruent triangles. As a result, the altitude cuts the base into two equal segments. The length of the altitude is 18 inches, and the length of the base is 15 in
An altitude is drawn from the vertex of an isosceles triangle, forming a right angle and two congruent triangles. As a result, the altitude cuts the base into two equal segments. The length of the altitude is 18 inches, and the length of the base is 15 in
- A right triangle
 A right triangle has legs with lengths of 24 cm and 21 cm if the length of the hypotenuse, in cm, can be written in the form of 3 sqrt(d), then what is the value of d?
A right triangle has legs with lengths of 24 cm and 21 cm if the length of the hypotenuse, in cm, can be written in the form of 3 sqrt(d), then what is the value of d? - In football
 In football, the path that a defender must run to tackle the ball carrier is called the path of pursuit. If the ball carrier runs 40 yards to the end zone and the path of pursuit is 45 yards; how far apart were the ball carrier and defender when they star
In football, the path that a defender must run to tackle the ball carrier is called the path of pursuit. If the ball carrier runs 40 yards to the end zone and the path of pursuit is 45 yards; how far apart were the ball carrier and defender when they star - Piece of a wire
 A piece of wire is bent into the shape of a triangle. Two sides have lengths of 24 inches and 21 inches. The angle between these two sides is 55°. What is the length of the third side to the nearest hundredth of an inch? A: The length of the third side is
A piece of wire is bent into the shape of a triangle. Two sides have lengths of 24 inches and 21 inches. The angle between these two sides is 55°. What is the length of the third side to the nearest hundredth of an inch? A: The length of the third side is - Parallelogram - right angles
 In parallelogram ABCD; AB = 16 cm, BC = 12 cm and diagonal AC = 20 cm. Find the area of the parallelogram.
In parallelogram ABCD; AB = 16 cm, BC = 12 cm and diagonal AC = 20 cm. Find the area of the parallelogram. - A lighthouse
 A lighthouse overlooks a bay, and it is 77 meters high. From the top, the lighthouse keeper can see a yacht southward at an angle of depression of 32 degrees and another boat eastward at an angle of 25 degrees. What is the distance between the boats?
A lighthouse overlooks a bay, and it is 77 meters high. From the top, the lighthouse keeper can see a yacht southward at an angle of depression of 32 degrees and another boat eastward at an angle of 25 degrees. What is the distance between the boats?
- The rhombus (a,d)
 Find the area of a rhombus, one side of which measures 20 cm, and one diagonal 24 cm.
Find the area of a rhombus, one side of which measures 20 cm, and one diagonal 24 cm. - A tree 3
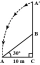 A tree breaks due to storm and the broken part bends so that the top of the tree touches the ground making an angle 30° with it. The distance between the foot of the tree to the point where the top touches the ground is 8 m. Find the height of the tree.
A tree breaks due to storm and the broken part bends so that the top of the tree touches the ground making an angle 30° with it. The distance between the foot of the tree to the point where the top touches the ground is 8 m. Find the height of the tree. - Grassland and goat
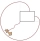 An unfenced grassland is a right triangle ABC with AB = 4m, BC = 8m, and AC as hypotenuse. A goat is tied to a 5-m long rope with its stake at point O, which is 2m from side AB and 2m from the prolongation of side BC through corner B. Then: 1. How far is
An unfenced grassland is a right triangle ABC with AB = 4m, BC = 8m, and AC as hypotenuse. A goat is tied to a 5-m long rope with its stake at point O, which is 2m from side AB and 2m from the prolongation of side BC through corner B. Then: 1. How far is - Two chords 2
 The length of one of two chords of a circle is 12cm. If the chords are 6cm and 7cm, respectively, away from the center of the circle, calculate the length of the second chord.
The length of one of two chords of a circle is 12cm. If the chords are 6cm and 7cm, respectively, away from the center of the circle, calculate the length of the second chord. - A baseball
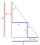 A baseball is hit over the 325 foot fence, which is 110 feet tall. How far did the ball carry on a straight line when it reached the fence?
A baseball is hit over the 325 foot fence, which is 110 feet tall. How far did the ball carry on a straight line when it reached the fence?
- Triangle 90
 Triangle made by 6 cm 4.5 cm and 7.5 cm. what angles does it make?
Triangle made by 6 cm 4.5 cm and 7.5 cm. what angles does it make? - Three inscribed objects
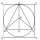 A circle is inscribed in a square. An equilateral triangle of side 4√3 is inscribed in that circle. Find the length of the diagonal of the square.
A circle is inscribed in a square. An equilateral triangle of side 4√3 is inscribed in that circle. Find the length of the diagonal of the square. - Parallel lines - dist
 Find the distance between the parallel lines 3x – 4y +7 = 0 and 3x – 4y + 5 = 0
Find the distance between the parallel lines 3x – 4y +7 = 0 and 3x – 4y + 5 = 0 - PQR - Euclid
 Find the length of line segment PR - leg of the right triangle PQR. PQ=17 cm PS=15 cm QS=8 cm; Point S is the height touch point with a hypotenuse of the RQ.
Find the length of line segment PR - leg of the right triangle PQR. PQ=17 cm PS=15 cm QS=8 cm; Point S is the height touch point with a hypotenuse of the RQ. - Trigonometric fx
 When an acute angle φ is in the standard position, its terminal side passes through point P (1,3). Find trigonometric functions of angle θ : sin φ, cos φ, tan φ, cotan φ.
When an acute angle φ is in the standard position, its terminal side passes through point P (1,3). Find trigonometric functions of angle θ : sin φ, cos φ, tan φ, cotan φ.
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
