Three inscribed objects
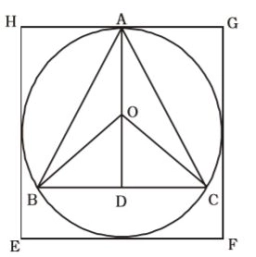
A circle is inscribed in a square. An equilateral triangle of side 4√3 is inscribed in that circle. Find the length of the diagonal of the square.
Final Answer:
Showing 1 comment:
Dr. Math
Okay, so there's a square, and inside it, there's a circle that fits perfectly (inscribed). Then, inside that circle, there's an equilateral triangle with each side measuring 4 √3 . I need to find the diagonal of the square.
First, let's visualize the shapes:
1. Square: Let's say the square has side length s .
2. Circle: Inscribed in the square, so its diameter is equal to the side of the square. Therefore, the radius r of the circle is s2 .
3. Equilateral Triangle: Inscribed in the circle, with each side 4 √3 .
I need to find the diagonal of the square, which is s √2 (since the diagonal of a square with side s is s √2 ).
So, my goal is to find s , and then calculate s √2 .
Step 1: Relate the Equilateral Triangle to the Circle
An equilateral triangle inscribed in a circle has a specific relationship between its side length and the radius of the circle.
For an equilateral triangle with side length a , the radius R of the circumscribed circle (circumradius) is given by:
In this problem, the side length a = 4 √3 , so:
Wait, that simplifies to:
So, the radius of the circle is 4.
Step 2: Relate the Circle to the Square
The circle is inscribed in the square, so the diameter of the circle is equal to the side length of the square.
Diameter of the circle = 2 × radius = 2 × 4 = 8
Therefore, the side length of the square s = 8
Step 3: Find the Diagonal of the Square
The diagonal d of a square with side length s is:
So, plugging in s = 8 :
Final Answer:
First, let's visualize the shapes:
1. Square: Let's say the square has side length s .
2. Circle: Inscribed in the square, so its diameter is equal to the side of the square. Therefore, the radius r of the circle is s2 .
3. Equilateral Triangle: Inscribed in the circle, with each side 4 √3 .
I need to find the diagonal of the square, which is s √2 (since the diagonal of a square with side s is s √2 ).
So, my goal is to find s , and then calculate s √2 .
Step 1: Relate the Equilateral Triangle to the Circle
An equilateral triangle inscribed in a circle has a specific relationship between its side length and the radius of the circle.
For an equilateral triangle with side length a , the radius R of the circumscribed circle (circumradius) is given by:
R = a √3
In this problem, the side length a = 4 √3 , so:
R = 4 √3 √3 = 4
Wait, that simplifies to:
R = 4 √3 √3 = 4
So, the radius of the circle is 4.
Step 2: Relate the Circle to the Square
The circle is inscribed in the square, so the diameter of the circle is equal to the side length of the square.
Diameter of the circle = 2 × radius = 2 × 4 = 8
Therefore, the side length of the square s = 8
Step 3: Find the Diagonal of the Square
The diagonal d of a square with side length s is:
d = s √2
So, plugging in s = 8 :
d = 8 √2
Final Answer:
8 √2
Tips for related online calculators
Check out our ratio calculator.
Do you want to convert length units?
See also our right triangle calculator.
Calculation of an equilateral triangle.
See also our trigonometric triangle calculator.
Do you want to convert length units?
See also our right triangle calculator.
Calculation of an equilateral triangle.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
algebraarithmeticplanimetricsbasic operations and conceptsUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Annular area
 The square with side a = 1 is inscribed and circumscribed by circles. Find the annular area.
The square with side a = 1 is inscribed and circumscribed by circles. Find the annular area. - Square inscribed
 Find the length of the side of the square ABCD, which is inscribed to a circle k with a radius of 10 cm.
Find the length of the side of the square ABCD, which is inscribed to a circle k with a radius of 10 cm. - Equilateral 5140
 I have a circle with a diameter of 6.4 cm. I need to find out the length of the side of an equilateral triangle inscribed in a circle.
I have a circle with a diameter of 6.4 cm. I need to find out the length of the side of an equilateral triangle inscribed in a circle. - Circumference 4278
 An inscribed circle is also described as an equilateral triangle with a side length of 8 cm. How many cm is the circumference of the inscribed circle smaller than the circumference of the described circle?
An inscribed circle is also described as an equilateral triangle with a side length of 8 cm. How many cm is the circumference of the inscribed circle smaller than the circumference of the described circle? - Two circles 3
 Two circles are inscribed in a square whose side is 4 cm. Find the radius of the smaller circle.
Two circles are inscribed in a square whose side is 4 cm. Find the radius of the smaller circle. - Described 4187
 Find the area of the circle that is a) inscribed, b) described 6.32 cm square.
Find the area of the circle that is a) inscribed, b) described 6.32 cm square. - ET inscribed circle
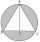 An equilateral triangle has been inscribed in a circle with a radius of 4 cm . Find the area of the shaded region.
An equilateral triangle has been inscribed in a circle with a radius of 4 cm . Find the area of the shaded region.
