Příklady na plocha pravoúhlého trojúhelníku - strana 2 z 9
Počet nalezených příkladů: 161
- Hippokratovy měsíčky.
Vypočítejte součet obsahů tzv. Hippokratových měsíčků, které byly setrojeny nad odvěsnami pravoúhlého trojúhelníka (a=6cm, b=8cm). Návod: vypočítejte nejprve obsahy polokruhů nad všemi stranami trojúhelníka ABC. Porovnejte součet obsahů měsíčků s obsahem - Trojúhelníku 60543
Základna pravoúhlého trojúhelníku je 10 centimetrů a nejdelší strana má 26 centimetrů. Jaká je plocha trojúhelníku? - Trojúhelníková 60023
Pravidelná trojúhelníková pyramida se sklonem 9 m má objem 50 m³. Najděte obsah boční stěny pyramidy. - Je dán 14
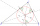Je dán trojúhelník ABC a kružnice vepsaná do tohoto trojúhelníka o poloměru 15. Bod T je bodem dotyku vepsané kružnice se stranou BC. Jaká je plocha trojúhelníka ABC jestliže |BT| = 25 a |TC| = 26?
- Rovnoramenném 53481
V rovnoramenném lichoběžníku ABCD známe: AB||CD, |CD| = c = 8 cm, výška h = 7 cm, | CAB| = 35°. Najděte obsah lichoběžníku. - Čtvercovou 46151
Vypočítej povrch jehlanu se čtvercovou podstavou o hraně délky 6cm a výšce 6cm. - Jak rozdělit
Jak rozdělit rovnoramenný trojúhelník na dvě části o stejných obsazích kolmo na osu souměrnosti (na lichoběžník a trojúhelník)? - Střecha
Střecha domu má tvar pravidelného čtyřbokého jehlanu o výšce 5 m a hraně podstavy 7 m. Kolik je třeba tašek o obsahu 540 cm²? - Lichoběžníku 44431
1. V kartézském rámci o funkcích f a g víme, že: funkce (f) je definována vztahem f (x) = 2x², funkce (g) je definována vztahem g (x) = x + 3, bod (O) je počátkem reference, bod (C) je průsečík grafu funkce (g) s osou pořadnice, body A a B jsou průsečíky
- Slunečník
Slunečník má tvar pláště šestibokého pravidelného jehlanu, jehož podstavná hrana a=6dm a výška v=25cm. Kolik látky je třeba na zhotovení slunečníku, počítáme-li na spoje a odpad 10%. - Potřebuji 44081 Střecha v podobě jehlanu, na domě s půdorysem čtverce má rozměry 12 x 12 m, v nejvyšším bodě výšku 2m. Kolik krytiny potřebuji zakoupit? Počítej s rezervou 10%.
- 4b jehlan 7
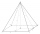Vypočítej povrch čtyřbokého jehlanu vysokého 3,5m s obdélníkovou podstavou s rozměry 3m a 1,8m. - Na louce
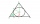Na louce přistála kosmická loď ve tvaru koule o průměru 6 m. Aby nepoutala pozornost, zakryli ji marťanci střechou ve tvaru pravidelného kužele. Jak vysoká bude tato střecha, aby spotřeba krytiny byla minimální? - Střecha Střecha věže má tvar pravidelného čtyřbokého jehlanu, jehož podstavná hrana je dlouhá 11 m a boční stěna svírá s podstavou úhel velikosti 57°. Vypočtěte kolik krytiny potřebujeme na pokrytí celé střechy, pokud počítáme s 15% -ním odpadem.
- Je dán 11
Je dán čtverec ABCD a bod E ležící vně daného čtverce. Jaká je plocha čtverce když platí že vzdálenost |AE| = 2, |DE| = 5 a |BE| = 4. - Komolý jehlan
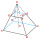Vypočtěte objem a povrch pravidelného čtyřbokého komolého jehlanu, jestliže a1 = 17 cm, a2 = 5 cm, výška v = 8 cm. - Pětiboký jehlan
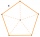Výška pravidelného pětibokého jehlanu je stejně dlouhá jako hrana podstavy, a to 20 cm. Vypočtěte objem a povrch jehlanu. - Zahrada
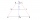Zahrada tvaru pravoúhlého lichoběžníku má základny délky 81m, 76m, a kolmé rameno 12m. Vypočtěte kolik m² plochy zůstane na výsadbu zeleně, pokud 1/3 plochy je zastavěná. Vypočtěte spotřebu pletiva na oplocení pozemku. - Vypočtěte 12
Vypočtěte povrch a objem pravidelného devítibokého jehlanu, měří-li poloměr kružnice vepsané podstavě ρ= 12 cm a výška jehlanu je 24 cm
Stan ve tvaru kužele je vysoký 3 m, průměr jeho podstavy je 3,2 m. a) Stan je vyroben je ze dvou vrstev materiálu. Kolik m² látky třeba na výrobu (včetně podlahy), pokud k minimálnímu množství třeba kvůli odpadu při stříhání přidat 20%? b) Kolik m³ vzduchMáš úkol, nad kterým si lámeš alespoň 10 minut hlavu? Pošli nám úkol a my Ti ji zkusíme vypočítat. Řešení příkladů z matematiky.
