V pravidelném 5
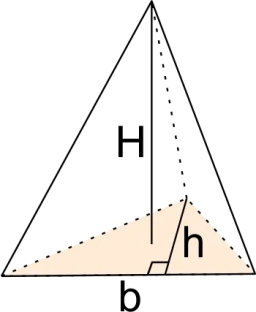
V pravidelném trojbokém jehlanu ABCV je odchylka boční stěny a roviny podstavy α = 45°. Určete odchylku boční hrany a roviny podstavy.
Správná odpověď:
Zobrazuji 1 komentář:
Dr. Math
V pravidelném trojbokém jehlanu ABCV je odchylka boční stěny a roviny podstavy α = 45°. Určete odchylku boční hrany a roviny podstavy.
Řešení:
1. Popis jehlanu:
- Pravidelný trojboký jehlan ABCV
- Podstava: rovnostranný trojúhelník ABC
- Vrchol: V
2. Značení:
- Odchylka boční stěny (např. ABV) od podstavy: α = 45°
- Hledáme odchylku boční hrany (např. AV) od podstavy: β = ?
3. Výpočet:
a) Označíme:
- a = délka strany podstavy
- v = výška podstavy = (a√3)/2
- h = výška jehlanu
- s = délka boční hrany
b) Pro odchylku boční stěny:
tan(α) = h / (v/3) = 3h/v
Pro α = 45°: 3h/v = 1 ⇒ h = v/3 = (a√3)/6
c) Pro odchylku boční hrany:
sin(β) = h/s
Nejprve spočteme s = √(h² + (2v/3)²) = √[(a√3/6)² + (a√3/3)²] = √(a²/12 + a²/3) = a√(5/12)
Pak sin(β) = (a√3/6) / (a√(5/12)) = √(3/5)/2 = √(15)/10
β = arcsin(√15 / 10) ≈ 37.76°
Odchylka boční hrany AV od roviny podstavy je β = arcsin(√15 / 10) ≈ 37.76°.
Řešení:
1. Popis jehlanu:
- Pravidelný trojboký jehlan ABCV
- Podstava: rovnostranný trojúhelník ABC
- Vrchol: V
2. Značení:
- Odchylka boční stěny (např. ABV) od podstavy: α = 45°
- Hledáme odchylku boční hrany (např. AV) od podstavy: β = ?
3. Výpočet:
a) Označíme:
- a = délka strany podstavy
- v = výška podstavy = (a√3)/2
- h = výška jehlanu
- s = délka boční hrany
b) Pro odchylku boční stěny:
tan(α) = h / (v/3) = 3h/v
Pro α = 45°: 3h/v = 1 ⇒ h = v/3 = (a√3)/6
c) Pro odchylku boční hrany:
sin(β) = h/s
Nejprve spočteme s = √(h² + (2v/3)²) = √[(a√3/6)² + (a√3/3)²] = √(a²/12 + a²/3) = a√(5/12)
Pak sin(β) = (a√3/6) / (a√(5/12)) = √(3/5)/2 = √(15)/10
β = arcsin(√15 / 10) ≈ 37.76°
Odchylka boční hrany AV od roviny podstavy je β = arcsin(√15 / 10) ≈ 37.76°.
Tipy na související online kalkulačky
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte si převody jednotek úhlů úhlové stupně, minuty, sekundy, radiány.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte si převody jednotek úhlů úhlové stupně, minuty, sekundy, radiány.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
- algebra
- vyjádření neznámé ze vzorce
- aritmetika
- odmocnina
- stereometrie
- jehlan
- planimetrie
- pravoúhlý trojúhelník
- trojúhelník
- goniometrie a trigonometrie
- arkussinus
Jednotky fyzikálních veličin:
Úroveň náročnosti úkolu:
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1
Související a podobné příklady:
- Pravidelný 8
 Pravidelný čtyřboký jehlan má podstavnou hranu a=1,56 dm a výšku v= 2,05dm. Vypočtěte : a) odchylku roviny boční stěny od roviny podstavy b) odchylku boční hrany od roviny podstavy
Pravidelný čtyřboký jehlan má podstavnou hranu a=1,56 dm a výšku v= 2,05dm. Vypočtěte : a) odchylku roviny boční stěny od roviny podstavy b) odchylku boční hrany od roviny podstavy - Výška = hrana
 V pravidelném čtyřboký jehlanu se výška boční stěny rovná délce hrany podstavy. Obsah boční stěny je 32 cm². Jaký je povrch jehlanu?
V pravidelném čtyřboký jehlanu se výška boční stěny rovná délce hrany podstavy. Obsah boční stěny je 32 cm². Jaký je povrch jehlanu? - Věž
 Kolik metrů čtverečních je potřeba na pokrytí věže tvaru pravidelného čtyřbokého jehlanu o podstavné hraně 10 metrů, je-li odchylka boční hrany od roviny podstavy 68°? Při pokrytí se počítá s odpadem 10%.
Kolik metrů čtverečních je potřeba na pokrytí věže tvaru pravidelného čtyřbokého jehlanu o podstavné hraně 10 metrů, je-li odchylka boční hrany od roviny podstavy 68°? Při pokrytí se počítá s odpadem 10%. - Věž
 Vypočtěte povrch pravidelného čtyřbokého jehlanu, jehož podstavná hrana měří 6 cm, je-li odchylka roviny boční stěny od roviny podstavy 50 stupňů.
Vypočtěte povrch pravidelného čtyřbokého jehlanu, jehož podstavná hrana měří 6 cm, je-li odchylka roviny boční stěny od roviny podstavy 50 stupňů.
- Úhel úhlopříčky
 V pravidelném 4-bokem jehlanu zvíře boční hrana s úhlopříčkou podstavy úhel 55°. Délka boční hrany je 8 m. Vypočtěte povrch a objem jehlanu.
V pravidelném 4-bokem jehlanu zvíře boční hrana s úhlopříčkou podstavy úhel 55°. Délka boční hrany je 8 m. Vypočtěte povrch a objem jehlanu. - Pravidelného 4905
 Květinový záhon má tvar pravidelného 4-bokého jehlanu. Hrana dolní podstavy je 10m, horní podstavy je 9m. Odchylka boční stěny od podstavy je 45 stupňů. Kolik sázení je třeba nakoupit, pokud k vysazení 1m čtverečního je třeba 90?
Květinový záhon má tvar pravidelného 4-bokého jehlanu. Hrana dolní podstavy je 10m, horní podstavy je 9m. Odchylka boční stěny od podstavy je 45 stupňů. Kolik sázení je třeba nakoupit, pokud k vysazení 1m čtverečního je třeba 90? - Osmiboký jehlan
 Urči objem pravidelného osmibokého jehlanu, jehož výška v = 100 a úhel boční hrany s rovinou podstavy je α = 60°.
Urči objem pravidelného osmibokého jehlanu, jehož výška v = 100 a úhel boční hrany s rovinou podstavy je α = 60°.
