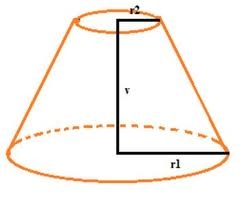
Komolý kužel
Kužel s poloměrem podstavy 12 cm a výškou 20 cm byl ve vzdálenosti 6 cm od podstavy seříznutý, čímž vznikl komolý kužel. Zjistěte poloměr podstavy komolého kužele.
Správná odpověď:
Tipy na související online kalkulačky
Vyzkoušejte naši kalkulačka na přepočet poměru.
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Související a podobné příklady:
- Seříznutý kužel
Vypočítejte objem komolého kužele s poloměry podstáv r1=18 cm, r2 = 9 cm a výškou v = 18 cm. - Lampa
Vypočtěte povrch lampového stínítka tvaru rotačního komolého kužele s průměry podstav 32 cm a 12 cm a výškou 24 cm. - Velký kužel
Seříznutý rotační kužel má podstavy s poloměry r1 = 8 cm, r2 = 4 cm a výšku v = 5 cm. Jaký je objem kužele, ze kterého komolý kužel vznikl? - Seříznutý kužel
Objem seříznutého kužele je V=38000π cm³. Poloměr dolní podstavy je o 10 cm větší, než poloměr horní podstavy. Určete poloměr podstav, pokud výška v=60 cm.
- Seříznutý kužel
Vypočítejte povrch a objem seříznutého rotačního kužele s poloměry podstav 14cm a 8cm, výškou 11cm. - Objem kužele
Vypočítejte objem kužele s poloměrem podstavy r a výškou v. a) r = 6 cm, v = 8 cm b) r = 0,9 m, v = 2,3 m c) r = 1,4 dm, v = 30 dm - Komolý kužel Výška kužele je 7 cm a délka boční strany je 10 cm a spodní poloměr je 3 cm. Jaká by mohla být odpověď na horní poloměr komolého kužele?
