Krejčí 4
Ze zbytku látky mohl rozstříhat buď po 3m na pánské obleky bez vest anebo po 3,6m na pánské obleky s vestami.
Jakou nejkratší možnou délku mohl mít zbytek látky v balíku?
Kolik obleků
a) bez vest
b) s vestami mohl krejčí ze zbytku látky ušít?
Jakou nejkratší možnou délku mohl mít zbytek látky v balíku?
Kolik obleků
a) bez vest
b) s vestami mohl krejčí ze zbytku látky ušít?
Správná odpověď:

Tipy na související online kalkulačky
Chceš si vypočítat nejmenší společný násobek dvou nebo více čísel?
Chcete proměnit jednotku délky?
Chcete převést dělení přirozených čísel - zjistit podíl a zbytek?
Chcete proměnit jednotku délky?
Chcete převést dělení přirozených čísel - zjistit podíl a zbytek?
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Jednotky fyzikálních veličin:
Úroveň náročnosti úkolu:
Související a podobné příklady:
- Krejčí 5
 Krejčí odhadl zbytek látky v balíku na 11 m. Měřením zjistil, že z této látky může nastříhat beze zbytku stejné kusy po 150 cm nebo po 210 cm. Kolik metrů látky bylo v balíku?
Krejčí odhadl zbytek látky v balíku na 11 m. Měřením zjistil, že z této látky může nastříhat beze zbytku stejné kusy po 150 cm nebo po 210 cm. Kolik metrů látky bylo v balíku? - Z balíku
 Z balíku, ve kterém bylo 30 metrů látky, odstřihl krejčí na ušití pracovních plášťů devětkrát po 285 centimetrech látky. Kolik metrů látky zbylo?
Z balíku, ve kterém bylo 30 metrů látky, odstřihl krejčí na ušití pracovních plášťů devětkrát po 285 centimetrech látky. Kolik metrů látky zbylo? - Vnitřní úhly
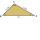 Vnitřní úhly trojúhelníku mají velikosti 30°, 45°, 105°, jeho nejdelší strana měří 10cm. Vypočítejte délku nejkratší strany, výsledek uveďte v cm s přesností na dvě desetinná čísla.
Vnitřní úhly trojúhelníku mají velikosti 30°, 45°, 105°, jeho nejdelší strana měří 10cm. Vypočítejte délku nejkratší strany, výsledek uveďte v cm s přesností na dvě desetinná čísla. - Spotřebuje 7021
 Kolik obleků ušijeme ze 40m látky, pokud se na jeden oblek spotřebuje 3 3/4 m látky?
Kolik obleků ušijeme ze 40m látky, pokud se na jeden oblek spotřebuje 3 3/4 m látky?
- Je dán 3
 Je dán kruh K s poloměrem r=8 cm. Jak velký poloměr musí mít menší soustředná kružnice, která rozdělí kruh K na dvě části se stejným obsahem?
Je dán kruh K s poloměrem r=8 cm. Jak velký poloměr musí mít menší soustředná kružnice, která rozdělí kruh K na dvě části se stejným obsahem? - V balíku 2
 V balíku je méně než 50 m látky. Budeme-li stříhat jen na blůzy nebo jen na šaty, nezůstane nám žádný zbytek. Na jednu blůzu se spotřebuje 1,5 m látky, na jedny šaty 3,2 m. Určete množství látky v balíku.
V balíku je méně než 50 m látky. Budeme-li stříhat jen na blůzy nebo jen na šaty, nezůstane nám žádný zbytek. Na jednu blůzu se spotřebuje 1,5 m látky, na jedny šaty 3,2 m. Určete množství látky v balíku. - Dovolená - stan
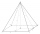 Ivan a Katka objevili na dovolené pravidelný jehlan, jehož podstavou byl čtverec se stranou 230 m a jehož výška byla rovna poloměru kruhu se stejným obsahem jako podstavný čtverec. Katka označila vrcholy čtverce ABCD. Ivan vyznačil na přímce spojující bod
Ivan a Katka objevili na dovolené pravidelný jehlan, jehož podstavou byl čtverec se stranou 230 m a jehož výška byla rovna poloměru kruhu se stejným obsahem jako podstavný čtverec. Katka označila vrcholy čtverce ABCD. Ivan vyznačil na přímce spojující bod
