Mařenka MO C-I-5
Mařenka rozmístí do vrcholů pravidelného osmiúhelníku různé počty od jednoho po osm bonbónů. Peter si pak může vybrat, které tři hromádky bonbónů dá Mařence, ostatní si ponechá. Jedinou podmínkou je, že tyto tři hromádky leží ve vrcholech rovnoramenného trojúhelníku. Mařenka chce rozmístit bonbóny tak, aby je dostala co nejvíce, ať už Peter trojici vrcholů vybere jakkoli. Kolik jich tak Mařenka zaručeně získá?
b) Stejnou roli vyřešte i pro pravidelný devítiúhelník, do kterého vrcholů rozmístí Mařenka 1 až 9 bonbónů. (Mezi rovnoramenné trojúhelníky řadíme i trojúhelníky rovnostranné.)
b) Stejnou roli vyřešte i pro pravidelný devítiúhelník, do kterého vrcholů rozmístí Mařenka 1 až 9 bonbónů. (Mezi rovnoramenné trojúhelníky řadíme i trojúhelníky rovnostranné.)
Správná odpověď:

Zobrazuji 1 komentář:
Leoyu10
Zdravím,
stále bych potřeboval nějaké podrobnější vysvětlení. Jak se vlastně dostanu k takovému výsledku? Děkuji za odpověď.
stále bych potřeboval nějaké podrobnější vysvětlení. Jak se vlastně dostanu k takovému výsledku? Děkuji za odpověď.
Tipy na související online kalkulačky
Vypočet rovnoramenného trojúhelníku.
Vypočet rovnostranného trojúhelníku.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vypočet rovnostranného trojúhelníku.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Jednotky fyzikálních veličin:
Téma:
Úroveň náročnosti úkolu:
Související a podobné příklady:
- Největší 79634
 V košíku je 12 jablek a 10 hrušek. Peter si má z nich vybrat buď jablko nebo hrušku tak, aby Víra, která si po něm vybere 1 jablko a 1 hrušku, měla co největší možnost výběru. Určete, co si Peter vybere.
V košíku je 12 jablek a 10 hrušek. Peter si má z nich vybrat buď jablko nebo hrušku tak, aby Víra, která si po něm vybere 1 jablko a 1 hrušku, měla co největší možnost výběru. Určete, co si Peter vybere. - Rozděl bonbóny
 Mamka koupila svým dětem balíček cukríkov. Všetkých 51 bonbónů z balíku rozdělila mezi svých 4 dětí tak, aby každé dítě dostalo co nejvíce a aby jí zůstalo co nejméně cukríkov. Kolik bonbónů zůstalo mamince?
Mamka koupila svým dětem balíček cukríkov. Všetkých 51 bonbónů z balíku rozdělila mezi svých 4 dětí tak, aby každé dítě dostalo co nejvíce a aby jí zůstalo co nejméně cukríkov. Kolik bonbónů zůstalo mamince? - Těžiště tetraeder
 Určete polohu těžiště soustavy čtyř hmotných bodů, které mají hmotnosti, m1, m2 = 2m1, m3 = 3M1 a m4 = 4m1, pokud leží ve vrcholech rovnoramenné tetraedru. (Ve všech případech mezi sousedními hmotnými body je vz
Určete polohu těžiště soustavy čtyř hmotných bodů, které mají hmotnosti, m1, m2 = 2m1, m3 = 3M1 a m4 = 4m1, pokud leží ve vrcholech rovnoramenné tetraedru. (Ve všech případech mezi sousedními hmotnými body je vz - Katka MO
 Katka narýsovala trojúhelník ABC. Střed strany AB si označila jako X a střed strany AC jako Y . Na straně BC chce najít takový bod Z, aby obsah čtyřúhelníku AXZY byl co největší. Jakou část trojúhelníku ABC může maximálně zabírat čtyřúhelník AXZY ?
Katka narýsovala trojúhelník ABC. Střed strany AB si označila jako X a střed strany AC jako Y . Na straně BC chce najít takový bod Z, aby obsah čtyřúhelníku AXZY byl co největší. Jakou část trojúhelníku ABC může maximálně zabírat čtyřúhelník AXZY ?
- Bonboniéra
 V bonboniéře je 12 bonbónů, které vypadají stejně. Tři z nich jsou plněné nugátem, čtyři oříškem a pět krémem. Nejméně kolik bonbónů musí Ivan vybrat, aby měl jistotu, že vybere dva se stejnou nádivkou? ...
V bonboniéře je 12 bonbónů, které vypadají stejně. Tři z nich jsou plněné nugátem, čtyři oříškem a pět krémem. Nejméně kolik bonbónů musí Ivan vybrat, aby měl jistotu, že vybere dva se stejnou nádivkou? ... - Předpokládejme 62424
 Deryl si chce ušetřit peníze, aby se zajistil do důchodu. Po uplynutí jednoho roku začne každý rok ukládat stejnou pevnou částku po dobu následujících 30 let na důchodový spořicí účet. Po uplynutí jednoho roku od provedení posledního vkladu vybere 100 000
Deryl si chce ušetřit peníze, aby se zajistil do důchodu. Po uplynutí jednoho roku začne každý rok ukládat stejnou pevnou částku po dobu následujících 30 let na důchodový spořicí účet. Po uplynutí jednoho roku od provedení posledního vkladu vybere 100 000 - Osmiúhelníku 66344
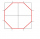 Ze čtverce o straně 4 cm odřízneme čtyři pravoúhlé rovnoramenné trojúhelníky s pravým úhlem ve vrcholech čtverce a s přeponou √2 cm. Dostaneme osmiúhelník. Vypočítejte jeho obvod, pokud plocha osmiúhelníku je 14cm².
Ze čtverce o straně 4 cm odřízneme čtyři pravoúhlé rovnoramenné trojúhelníky s pravým úhlem ve vrcholech čtverce a s přeponou √2 cm. Dostaneme osmiúhelník. Vypočítejte jeho obvod, pokud plocha osmiúhelníku je 14cm².
