Candy - MO
Gretel deploys different numbers to the vertex of a regular octagon, from one to eight candy. Peter can then choose which three piles of candy to give Gretel others retain. The only requirement is that the three piles lie at the vertices of an isosceles triangle. Gretel wants to distribute sweets so that they get as much as possible, whether Peter's trio vertices are chosen anyhow. How many such Gretel guaranteed profits?
b) Do the same task even for regular 9-gon to deploy Gretel 1-9 sweets. (Equilateral triangles are also isosceles triangles.)
b) Do the same task even for regular 9-gon to deploy Gretel 1-9 sweets. (Equilateral triangles are also isosceles triangles.)
Correct answer:

Tips for related online calculators
Calculation of an isosceles triangle.
Calculation of an equilateral triangle.
See also our trigonometric triangle calculator.
Calculation of an equilateral triangle.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Themes, topics:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Grandmother
 Grandmother wants to give the candies to grandchildren so that when she gives five candy everyone, three are missing, and when she gives four candies, 3 are surplus. How many grandchildren have a grandmother, and how many sweets do they have?
Grandmother wants to give the candies to grandchildren so that when she gives five candy everyone, three are missing, and when she gives four candies, 3 are surplus. How many grandchildren have a grandmother, and how many sweets do they have? - In an
 In an ABCD square, n interior points are chosen on each side. Find the number of all triangles whose vertices X, Y, and Z lie at these points and on different sides of the square.
In an ABCD square, n interior points are chosen on each side. Find the number of all triangles whose vertices X, Y, and Z lie at these points and on different sides of the square. - N points on the side
 An equilateral triangle A, B, and C on each of its inner sides lies N=13 points. Find the number of all triangles whose vertices lie at given points on different sides.
An equilateral triangle A, B, and C on each of its inner sides lies N=13 points. Find the number of all triangles whose vertices lie at given points on different sides. - Intersection 81017
 There are also two equilateral triangles ABC, and BDE, such that the size of the angle ABD is greater than 120° and less than 180° points C and E lie in the same half-plane defined by the line AD. The intersection of CD and AE is marked F. Determine the s
There are also two equilateral triangles ABC, and BDE, such that the size of the angle ABD is greater than 120° and less than 180° points C and E lie in the same half-plane defined by the line AD. The intersection of CD and AE is marked F. Determine the s
- Internal angles
 The ABCD is an isosceles trapezoid, which holds: |AB| = 2 |BC| = 2 |CD| = 2 |DA|: On the BC side is a K point such that |BK| = 2 |KC|, on its side CD is the point L such that |CL| = 2 |LD|, and on its side DA, the point M is such that | DM | = 2 |MA|. Det
The ABCD is an isosceles trapezoid, which holds: |AB| = 2 |BC| = 2 |CD| = 2 |DA|: On the BC side is a K point such that |BK| = 2 |KC|, on its side CD is the point L such that |CL| = 2 |LD|, and on its side DA, the point M is such that | DM | = 2 |MA|. Det - Triangles - combinations
 How many different triangles with sides in whole centimeters have a perimeter of 12 cm?
How many different triangles with sides in whole centimeters have a perimeter of 12 cm? - Quadrilateral 82395
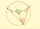 The points ABC lie on the circle k(S, r) such that the angle at B is obtuse. How large must the angle at vertex B of quadrilateral SCBA be so that this angle is three times greater than the interior angle ASC of the same quadrilateral?
The points ABC lie on the circle k(S, r) such that the angle at B is obtuse. How large must the angle at vertex B of quadrilateral SCBA be so that this angle is three times greater than the interior angle ASC of the same quadrilateral?
