Kombinatorické pravidlo súčinu - slovné úlohy a príklady - strana 25 z 28
Počet nájdených príkladov: 559
- Zápas v hokeji
Zápas v hokeji sa skončil výsledkom 3:1. Koľko rôznych priebehov mohol mať daný zápas? - Poháre
Mám 7 pohárov: 1 2 3 4 5 6 7. Koľko je možnosti postavenia pohárov ak 1 a 2 sú stále vedľa seba a môžu sa navzájom prehodiť? - Počet čísel
Nájdi počet všetkých trojciferných prirodzených čísel, ktoré sa dajú zostaviť z číslic 1,2,3,4 a pre ktoré platia súčasne ešte tieto podmienky: na mieste jednotiek je jedna z číslic 1,3,4, na mieste stoviek číslica 4 alebo 2 - V cukrárni
V cukrárni predávajú 5 druhov zmrzlín. Koľkými spôsobmi si môžem kúpiť 3 druhy, ak mi na poradí zmrzlín nezáleží?
- Cestovná kancelária
Malá cestovná kancelária ponúka 5 rôznych zájazdov na medové týždne. Aká je pravdepodobnosť, že aj nevesta aj ženích si zvolia ten istý zájazd (predpokladame, že si vyberajú nezávisle)? - Jedna zelená
V nádobe je 45 bielych a 15 zelených guličiek. Náhodne vyberieme 5 guličiek. Aká je pravdepodobnosť, že bude maximálne jedna zelená? - Trojciferné
Koľko prirodzených trojciferných čísel je väčších ako 321, ak sa žiadna číslica v číslach neopakuje? - Priamky
V koľkých bodoch sa pretína 9 priamok v rovine, z ktorých 4 sú navzájom rovnobežné a z ostatných 5 žiadne dve nie sú rovnobežné (a ak predpokladáme, že každým priesečníkom prechádzajú len dve priamk)? - Ako fungujú senáty
Rozhodovacia komisia je tvorená troma ľuďmi. Aby bolo rozhodnutie komisie plátne, je nutné, aby najmenej dvaja členovia hlasovali rovnako. V komisii nieje možné nehlasovať, každý hlasuje iba áno, alebo nie. Predpokladáme, že prví dvaja členovia komisie sú
- Kamaráti
5 kamarátov šlo do kina. Koľkými možnými spôsobmi sa môžu usadiť vedľa seba v jednom rade, ak jeden z nich chce sedieť v strede a tým zvyšným na mieste nezáleží? - Tábor
Na konci tábora si 10 kamaráti navzájom vymenili adresy. Každý dal zvyšným 9 kamarátom svoju vizitku. Koľko adries si vymenili? - Trojciferné čísla
Z číslic 1, 2, 3, 4, 5 utvor všetky trojciferné čísla tak, aby sa v nich neopakovala žiadna číslica a aby číslo bolo deliteľné číslom 2. Koľko je takých čísel? - Trojmiestne čísla
Koľko je trojciferných prirodzených čísel takých, že sa v nich žiadna číslica neopakuje? - Šachy
Koľkými možnými spôsobmi sa dá začať šachová partia (prvý ťah)?
- Kombinácie
Koľko je rôznych kombinácií 2-ciferného čísla delitelného číslom 4 vzniknutého z číslic 3, 5 a 7? - Trojciferné
Určte počet všetkých kladných trojciferných čísiel, ktoré obsahujú číslicu 7. - Sedemsegmentovka
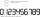Lenka sa bavila tým, že vyťukávala na kalkulačke (sedemsegmentový displej) čísla, pričom používala iba číslice od 2 do 9. Zápisy niektorých čísel mali tú vlastnosť, že ich obraz v osovej alebo stredovej súmernosti bol opäť zápisom nejakého čísla. Určte po - Hokejisti
Po vystriedaní si na striedačke náhodne sadlo vedľa seba päť hokejistov. Aká je pravdepodobnosť, že dvaja najlepší strelci z tejto pätice budú sedieť vedľa seba? - Tréningy
V tabuľke je harmonogram sobotňajších tenisových tréningov mladších žiakov počas zimnej halovej sezóny. Pred začiatkom letnej sezóny sa pripravuje nový harmonogram tréningov. Tomáš Kučera bude môcť trénovať len predpoludním, sestry Kováčové budú musieť tr
Písmenkový Logik je hra pre dvoch hráčov, ktorá má nasledujúce pravidlá: 1. Prvý hráč si myslí pětipísmenné slovo, v ktorom sa žiadne písmeno neopakuje. 2. Druhý hráč napíše nejaké 5-písmenné slovo. 3. Prvý hráč odpovie dvoma číslami - prvé číslo udáva, kMáš úlohu, nad ktorou si lámeš aspoň 10 minút hlavu? Pošli nám úlohu a my Ti ju skúsime vypočítať. Riešenie príkladov z matematiky.
