Tangent - practice problems
Tangent is a trigonometric function. In a rectangular triangle, it is the ratio of the opposite and adjacent side to a given internal angle. Algebraically is defined as the ratio of the sine and cosine of a given angle. It is periodic with a period of π = 180 °.Number of problems found: 292
- The shadow 2
The shadow of a tower standing on a level ground is found to be 40 m longer when the Sun’s altitude is 30° than when it is 60°. Find the height of the tower. - Angle over circle
In the figure, O is the center of the circle and AB is tangent at B. If angle OAB is 28 degrees find angle AOB. Figure is not scaled. - Angle of inclination
Find the angle of inclination of a ramp that rise for 80 cm and is 200 cm long. - Tower + pole
On the horizontal plane, there is a vertical tower with a flag pole on its top. At a point 9 m away from the foot if the tower, the angle of elevation of the top and bottom of the flag pole are 60°and 30° respectively. Find the height of the flag pole.
- A tree 3
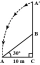A tree breaks due to storm and the broken part bends so that the top of the tree touches the ground making an angle 30° with it. The distance between the foot of the tree to the point where the top touches the ground is 8 m. Find the height of the tree. - The angle 9
The angle of elevation of the top of a tower from a point A on the ground is 30°. On moving a distance of 20 m towards the foot of the tower to a point B, the angle of elevation increases to 60°. Find the height of the tower and the distance of the tower - Angle and slope
Find the angle between the x-axis and the line joining the points (3, -1) and (4,-2) . - Angle of elevation
From a point A on the ground, the angle of elevation of the top of a 20 m tall of a building is 45°. A flag is hoisted at the top of the building and the angle of elevation of the top of the flagstaff from A is 60°. Find the length of the flagstaff and th - Two men 2
Two men are on opposite sides of a tower. They measure the angles of elevation of the top of the tower as 30° and 45°, respectively. If the height of the tower is 50 m, find the distance between the two men.
- RT with rectangle
In the diagram, find the lengths h and b. One rectangle and one right triangle share one side. We know two angles and the length of the common side, as shown in the picture. - A man 23
A man standing on the deck of a ship, which is 10 m above the water level, observes the angle of elevation of the top of a hill as 60°, and angle of depression of the base of the hill is 30°. Find the distance of the hill from the ship and the height of t - Angle of elevation
The angle of elevation of the top of an unfinished pillar at a point 150 m from its base is 30°. If the angle of elevation at the same point is to be 45°, then the pillar has to be raised to a height of how many meters? - A lighthouse
A lighthouse overlooks a bay, and it is 77 meters high. From the top, the lighthouse keeper can see a yacht southward at an angle of depression of 32 degrees and another boat eastward at an angle of 25 degrees. What is the distance between the boats? - The apothem
The apothem of a regular hexagon is 5√3 inches. Find one of its sides and area.
- One side 4
One side of a regular octagon is 12 inches. Find the apothem and its area. - A boy 5
A boy starts at A and walks 3km east to B. He then walks 4km north to C. Find the bearing of C from A. - A radio antenna
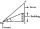Avanti is trying to find the height of a radio antenna on the roof of a local building. She stands at a horizontal distance of 21 meters from the building. The angle of elevation from her eyes to the roof (point A) is 42°, and the angle of elevation from - A right
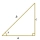A right triangle has side lengths a=3, b=5, and c=4, as shown below. Use these lengths to find tan x, sin x, and cos x. - Subtract polar forms
Solve the following 5.2∠58° - 1.6∠-40° and give answer in polar form
Let z = 2 - sqrt(3i). Find z6 and express your answer in rectangular form. if z = 2 - 2sqrt(3 i) then r = |z| = sqrt(2 ^ 2 + (- 2sqrt(3)) ^ 2) = sqrt(16) = 4 and theta = tan -2√3/2=-π/3Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
