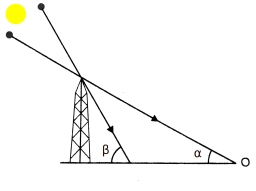
The shadow 2
The shadow of a tower standing on a level ground is found to be 40 m longer when the Sun’s altitude is 30° than when it is 60°. Find the height of the tower.
Correct answer:
Tips for related online calculators
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- The angle 9
The angle of elevation of the top of a tower from a point A on the ground is 30°. On moving a distance of 20 m towards the foot of the tower to a point B, the angle of elevation increases to 60°. Find the height of the tower and the distance of the tower - A man 23
A man standing on the deck of a ship, which is 10 m above the water level, observes the angle of elevation of the top of a hill as 60°, and angle of depression of the base of the hill is 30°. Find the distance of the hill from the ship and the height of t - TV tower
Calculate the height of the television tower if an observer standing 430 m from the base of the tower sees the peak at an altitude angle of 23°. - Elevation 80866
Find the height of the tower when the geodetic measured two angles of elevation α=34° 30'' and β=41°. The distance between places AB is 14 meters.
- A boy
A boy of 1.7m in height is standing 30m away from the flagstaff on the same level ground. He observes that the angle of deviation of the top of the flagstaff is 30 degrees. Calculate the height of the flagstaff. - The chimney
The chimney casts a shadow 45 meters long. The one-meter-long rod standing perpendicular to the ground has a shadow 90 cm long. Calculate the height of the chimney. - Sun rays
If the sun's rays are at an angle of 60°, then the famous Great Pyramid of Egypt (which is now 137.3 meters high) has a 79.3 m long shadow. Calculate the current height of the neighboring Chephren pyramid, whose shadow is measured at the same time at 78.8
