Tangent - practice problems - page 2 of 15
Number of problems found: 292
- The tower
From a window 8 m above the horizontal plane, we can see the top of the tower at an elevation angle of 53 degrees 20 minutes, and its base at an angle of 14 degrees 15 minutes. How high is the tower? - Perpendicular 83636
In a right-angled triangle, you know a drop of 7 meters and an angle of 30 degrees. Calculate the type of overhang; calculate both variants - the specified angle is opposite and adjacent to the specified perpendicular. - Horizontal 83362
The observer sees the plane at an elevation angle of 35° (angle from the horizontal plane). At that moment, the plane reported an altitude of 4 km. How far from the observer is the place over which the aircraft flies? They circled for hundreds of meters. - Calculate 83261
Calculate the area of the triangle ABC, in which you know the side c=5 cm, the angle at the top A= 70 degrees, and the ratio of the segments cut by the height to the side c is 1:3
- Overhangs 83158
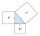The area of a right triangle ABC is 346 cm2, and the angle at vertex A is 64°. Calculate the lengths of the overhangs a and b. - Horizontal 83148
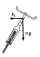The bend has a radius of r = 100 m and is inclined at an angle of 20° to the horizontal plane (= tilt angle). What is the safe (the "best") speed to go through this curve? Sketch the picture regarding NIVS, mark the forces, and calculate. - Determine 83083
A 6.5-meter-long ladder rests against a vertical wall. Its lower end rests on the ground 1.6 meters from the wall. Determine how high the top of the ladder reaches and at what angle it rests against the wall. - Difference 83079
On the traffic sign that informs about the road's gradient, the figure is 6.7%. Determine the slope angle of the path. What height difference is covered by the car that traveled 2.8 km on this road? - Height of poplar
From the 40 m high observation deck, you can see the top of the poplar at a depth angle of 50°10' and the bottom of the poplar at a depth angle of 58°. Calculate the height of the poplar.
- Observer's 82805 An airliner currently flying over a location 2,400 m away from the observer's location is seen at an elevation angle of 26° 20'. At what height does the plane fly?
- Observation 82708
At the top of the hill, there is a 30-meter-high observation tower. We can see its heel and shelter from a certain point in the valley at elevation angles a=28°30" and b=30°40". How high is the top of the hill above the horizontal plane of the observation - Calculate 82696
In the triangle ABC, b=5 cm, c=6 cm, /BAC/ = 80° are given. Calculate the sizes of the other sides and angles, and further determine the sizes of the tangent tc and the area of the triangle. - Mast angles and height
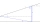Calculate the height of the mast, whose foot can be seen at a depth angle of 11° and the top at a height angle of 28°. The mast is observed from a position 10 m above the level of the base of the mast. - The tangent of the hyperbola
Write the equation of the tangent of the hyperbola 9x²−4y²=36 at the point T =[t1,4].
- Calculate 82567
The volume of a cuboid with a square base is 64 cm3, and the body diagonal deviation from the base's plane is 45 degrees. Calculate its surface area. - Coefficient 82566
What is the maximum angle at which the tram can go downhill to still be able to stop? The coefficient of shear friction is f =0.15. - Trapezoid 82216
Given is an isosceles trapezoid ABCD with bases 10 cm and 14 cm. The height of the trapezoid is 6 cm. Determine the interior angles of the trapezoid. - Vertically 82162
The pole is stuck vertically into the ground. The protruding length is 1m. What is the length of the shadow cast when the sun is just 50° above the horizon? - Quadrilateral 82146
Calculate the volume and surface area of a regular quadrilateral prism with base edge a=24 cm if the body diagonal makes an angle of 66° with the base.
The tangent of the angle formed by the adjacent sides of the triangle ABC (side a=29 m, b = 40 m) equals 1.05. Calculate the area of that triangle.Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
