Right triangle + length - practice problems
Number of problems found: 635
- A right triangle
A right triangle has legs with lengths of 24 cm and 21 cm if the length of the hypotenuse, in cm, can be written in the form of 3 sqrt(d), then what is the value of d? - An isosceles triangle
An altitude is drawn from the vertex of an isosceles triangle, forming a right angle and two congruent triangles. As a result, the altitude cuts the base into two equal segments. The length of the altitude is 18 inches, and the length of the base is 15 in - The vertices
The vertices of a triangle are A (-1,3), B (1,-1), and C (5, 1). Find the length of the median through the vertex C. - Mrs. Clarke
Mrs. Clarke is teaching a 5th-grade class. She is standing 40 feet in front of Valeria. Sarah is sitting to Valeria's right. If Sarah and Mrs. Clarke are 50 feet apart, how far apart are Valeria and Sarah?
- A tree 2
A tree is broken at a height of 6 m from the ground and its top touches the ground at a distance of 8 m from the base of the tree. Find the original height of the tree. - An equilateral triangle 2
If the sides of an equilateral triangle are increased by 2 meters, the area is increased by 7√3 square meters. Find the length of the side. - Missing side length Use the Pythagorean Theorem (a² + b²=c²) to find a unknown side length: a = 5; c = 13 ; b=?
- An electrician 7
An electrician has to repair an electric fault on a pole 4 meters in height. He needs to reach a point 1 m below the top. What should be the length of the ladder that he could use, when inclined at an angle 60° to the horizontal? - Two men 2
Two men are on opposite sides of a tower. They measure the angles of elevation of the top of the tower as 30° and 45°, respectively. If the height of the tower is 50 m, find the distance between the two men.
- A man 23
A man standing on the deck of a ship, which is 10 m above the water level, observes the angle of elevation of the top of a hill as 60°, and angle of depression of the base of the hill is 30°. Find the distance of the hill from the ship and the height of t - A kite 3
A kite is flying at a height of 60 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60°. Find the length of the string, assuming that there is no slack in th - The coordinates 3
The coordinates of two vertices of an equilateral triangle are (1,1) and (5,1). What are the coordinates of the third vertex? - Triangle 82 Triangle PQR has vertices located at (2, 2), (5, -4), and (-4, -1). What type of triangle is triangle PQR?
- Angle of elevation
From a point A on the ground, the angle of elevation of the top of a 20 m tall of a building is 45°. A flag is hoisted at the top of the building and the angle of elevation of the top of the flagstaff from A is 60°. Find the length of the flagstaff and th
- Angle of inclination
Find the angle of inclination of a ramp that rise for 80 cm and is 200 cm long. - A tree 3
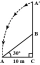A tree breaks due to storm and the broken part bends so that the top of the tree touches the ground making an angle 30° with it. The distance between the foot of the tree to the point where the top touches the ground is 8 m. Find the height of the tree. - A lighthouse
A lighthouse overlooks a bay, and it is 77 meters high. From the top, the lighthouse keeper can see a yacht southward at an angle of depression of 32 degrees and another boat eastward at an angle of 25 degrees. What is the distance between the boats? - RT with rectangle
In the diagram, find the lengths h and b. One rectangle and one right triangle share one side. We know two angles and the length of the common side, as shown in the picture. - Three inscribed objects
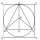A circle is inscribed in a square. An equilateral triangle of side 4√3 is inscribed in that circle. Find the length of the diagonal of the square.
Find the length of line segment PR - leg of the right triangle PQR. PQ=17 cm PS=15 cm QS=8 cm; Point S is the height touch point with a hypotenuse of the RQ.Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
