Reason - practice problems
Number of problems found: 2023
- Apples 32
A women sold half part of total apples to the 1st customer. Half part of the remaining to the 2nd customer. Then from rest of the apples she sold half part of it to the third customer and again sold half of the remaining apples to the forth customer. Now - Two trains 16
Two trains cross each other in 14 seconds when they are moving in opposite direction and when they are moving in the same direction they cross each other in 3 minutes 2 seconds . The speed of the faster train is by what percent more than the slower train? - A variable
A variable rectangle has a constant area of 35 cm². Find the lengths of the sides when the perimeter is minimum. - Three people
Three people - Peter, Quinton and Roland. 5 years ago, the average age of P and Q was 15 years. Present average age of P, Q and R is 20 years. Find the age of R after 10 years.
- Monthly income
There are three working people - X, Y, Z. The average monthly income of X and Y is 5050 USD.The average monthly income of Y and Z is 6250 USD, and the average monthly income of X and Z is 5200 USD. What is monthly income of X? - Common work 39 men can repair a road in 12 days working 5 hours a day. How many days will be required to complete the work by 30 men working 6 hours a day?
- Big school 2
The ratio of the number of boys to the number of girls in a school of 450 pupil is 4 : 5 . When some new boys and girls are admitted, the number of boys increases by 25 and ratio of boys and girls changes to 9 : 13 . Calculate the number of new girls admi - Palidrom
A number consists of two digits whose product is 24. When 18 is subtracted from the number, the digits change their places. Find the number. - Clock error
How much does a watch lose per day, if its hands coincide every 64 minutes?
- Minimum interior angle
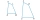What is the minimum interior angle possible for a regular polygon? - 4th digit Write a digit in place of X so that 85X634 is divisible by 11.
- A train 4
A train passes two bridges of 400 m and 260 m in 25 sec and 18 sec, respectively. Find the length and speed of the train. - Milk bottles
A container of milk was 4/5 full. When 12 bottles of milk were taken out and 8 bottles of milk poured into it, it was 3/4 full.How many bottles of milk can the container contain? - Full-tank
A full-tank of petrol a car lasts for 10 days. If driver starts using 25% more everyday, how many days will the full-tank petrol last?
- A mobile
A mobile phone and a tablet were sold at a profit of 10% and a loss of 8% respectively . If the cost price of the mobile is 1.5 times that of the tablet what is the overall percentage earned by selling both the articles? - A contractor 2 A contractor has to complete his contract in 92 days. 234 men were set to do the work, each of them works for 16 hours/day. After 66 days, 4/7 of the work is completed. How many additional men may be employed, so that the work may be completed in time, ea
- Multiple and remainder What is the least multiple of 7, which, when divided by each one of 6,9,15,18, gives the remainder of 4 in each case?
- Sport field
There is a circular path around a sports field. Sonia takes 18 minutes to drive one round of the field, while Roland takes 12 minutes for the same. Suppose they both start at the same point and at the same time and go in the same direction. After how many - What will
What will be the average of the numbers from 1 to 51?
In a group of cows and hens, the number of legs is 14, more than twice the number of heads. Find the number of cows.Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
