Practice problems of the circle
A circle is a geometric shape that consists of all points that are a fixed distance, called the radius, away from a central point called the center. The distance around the circle is called the circumference and the region enclosed by the circle is called the area of the circle. The formula for the circumference of a circle is C = 2πr, where C is the circumference, r is the radius, and π is a mathematical constant, the Ludolph number, approximately equal to 3.1415926.The formula for the area of a circle is A = πr2, where A is the area and r is the radius.
The diameter of a circle is a line segment that passes through the center of the circle and has its endpoints on the circle. It is the longest distance across the circle and is also twice the length of the radius. The formula for the diameter of a circle is d = 2 * r, where d is the diameter and r is the radius. The diameter of a circle is an important measurement in geometry and is used in many mathematical formulas, such as the formula for the circumference of a circle (C = πd)
Number of problems found: 948
- The diameter 5
 The diameter of a circle is 32 inches. What is the circle's area? Use π(pi) ≈ 3.14 and round your answer to the nearest hundredth.
The diameter of a circle is 32 inches. What is the circle's area? Use π(pi) ≈ 3.14 and round your answer to the nearest hundredth. - Concentric circles 4
 One circle has a radius of 98 cm, and a second concentric circle has a 1m 26 cm radius. How much longer is the circumference of the second circle than that of the first?
One circle has a radius of 98 cm, and a second concentric circle has a 1m 26 cm radius. How much longer is the circumference of the second circle than that of the first? - The radius 2
 The radius of a circle is increased by 5%. What is the percentage increase in their circumference area?
The radius of a circle is increased by 5%. What is the percentage increase in their circumference area? - Planetary system
 Robert has built a mechanical model solar system with three balls representing planets at the end of rods. Each rod is attached to the center, representing the Sun. The planets are lined up when he turns on the motor. The innermost planet makes a revoluti
Robert has built a mechanical model solar system with three balls representing planets at the end of rods. Each rod is attached to the center, representing the Sun. The planets are lined up when he turns on the motor. The innermost planet makes a revoluti
- Find all 2
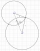 Find all the complex solutions (write the answer in the form x+iy) of the system. {|z-12|/|z-8i|=5/3 ; |z-4|=|z-8|
Find all the complex solutions (write the answer in the form x+iy) of the system. {|z-12|/|z-8i|=5/3 ; |z-4|=|z-8| - Circle inscribed square
 What is the area of the circle that can be inscribed in a square of 10 cm?
What is the area of the circle that can be inscribed in a square of 10 cm? - Pizza diameter
 If an 18-inch pizza costs $16.99 and is cut into 12 slices, what is the cost per square inch?
If an 18-inch pizza costs $16.99 and is cut into 12 slices, what is the cost per square inch? - Merly
 Merly prepared the table for lunch. She put a place mat that measures 5 dm long and 3 dm wide; she placed a plate on it with a diameter of 3 dm. How many mats can be seen on the table?
Merly prepared the table for lunch. She put a place mat that measures 5 dm long and 3 dm wide; she placed a plate on it with a diameter of 3 dm. How many mats can be seen on the table? - ET inscribed circle
 An equilateral triangle has been inscribed in a circle with a radius of 4 cm . Find the area of the shaded region.
An equilateral triangle has been inscribed in a circle with a radius of 4 cm . Find the area of the shaded region.
- Garden hose
 Miguel wound a garden hose around a circular real. If the diameter of the real is 10 inches, how many inches of hose was wound on the first full turn of the real round? The answer to the nearest whole inch, use 3.14 for pi.
Miguel wound a garden hose around a circular real. If the diameter of the real is 10 inches, how many inches of hose was wound on the first full turn of the real round? The answer to the nearest whole inch, use 3.14 for pi. - A cone 3
 A cone has a diameter of x cm and a slant height of y cm. A square pyramid has a base side length of x cm and a slant height of y cm. Which has the greater surface area? Explain.
A cone has a diameter of x cm and a slant height of y cm. A square pyramid has a base side length of x cm and a slant height of y cm. Which has the greater surface area? Explain. - Circular garden 2
 What is the area of the circular garden if the diameter of the circular garden is 4 meters?
What is the area of the circular garden if the diameter of the circular garden is 4 meters? - Two chords 2
 The length of one of two chords of a circle is 12cm. If the chords are 6cm and 7cm, respectively, away from the center of the circle, calculate the length of the second chord.
The length of one of two chords of a circle is 12cm. If the chords are 6cm and 7cm, respectively, away from the center of the circle, calculate the length of the second chord. - The minute
 The minute hand of a clock is 6 cm long. Find the area it sweeps between 2:05 PM and 2:40 PM.
The minute hand of a clock is 6 cm long. Find the area it sweeps between 2:05 PM and 2:40 PM.
- Geometric Solid
 A concrete pipe is 1.0 m long. Its inside and outside diameters are 60 cm and 75 cm, respectively. What is the volume of the concrete (cubic meters) needed to make 25 pcs of pipe?
A concrete pipe is 1.0 m long. Its inside and outside diameters are 60 cm and 75 cm, respectively. What is the volume of the concrete (cubic meters) needed to make 25 pcs of pipe? - Two chords 6
 A chord PQ is 10.4cm long, and its distance from the center of a circle is 3.7cm. Calculate the length of a second chord RS, which is 4.1cm from the center of this circle.
A chord PQ is 10.4cm long, and its distance from the center of a circle is 3.7cm. Calculate the length of a second chord RS, which is 4.1cm from the center of this circle. - Circle graph
 Erica surveyed students at her school about their favorite type of music. She made a circle graph to show the results. The central angle for the section of the graph that represents country music measures 72°. If 45 classmates chose the country as their f
Erica surveyed students at her school about their favorite type of music. She made a circle graph to show the results. The central angle for the section of the graph that represents country music measures 72°. If 45 classmates chose the country as their f - A goat 2
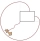 As shown, a goat is tied at one corner of a rectangular shed by a 5-meter-long rope. The shed measures 3 m by 2 m and is surrounded by grassland. What is the area of the grassland in which the goat can graze? Give your answer to the nearest m².
As shown, a goat is tied at one corner of a rectangular shed by a 5-meter-long rope. The shed measures 3 m by 2 m and is surrounded by grassland. What is the area of the grassland in which the goat can graze? Give your answer to the nearest m². - The diameter
 The diameter of a circle is 4 feet. What is the circle's circumference?
The diameter of a circle is 4 feet. What is the circle's circumference?
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
