Practice problems of the triangle
A triangle is a polygon with three edges and three vertices. It is one of the basic shapes in geometry. The sum of the measures of the interior angles of a triangle is always 180 degrees. An exterior angle of a triangle is an angle that is a linear pair (and hence supplementary) to an interior angle. The best known area formula is T = a*h /2 where a is the length of the side of the triangle, and h is the height or altitude of the triangle.Number of problems found: 2334
- Angles - triangle
 Find the measure of the angles of the triangle ABC if: the measure of angle A is the measure of angle C and the measure of angle B =½ of the measure of angle C.
Find the measure of the angles of the triangle ABC if: the measure of angle A is the measure of angle C and the measure of angle B =½ of the measure of angle C. - A triangle 8
 A triangle has a base of 9.2 feet and a height of 4.8 feet. What is the area of the triangle?
A triangle has a base of 9.2 feet and a height of 4.8 feet. What is the area of the triangle? - The angles 5
 The angles of a triangle are in arithmetic progression (AP). The greatest angle is twice the least. Find all the angles.
The angles of a triangle are in arithmetic progression (AP). The greatest angle is twice the least. Find all the angles. - Know one angle
 In a right-angled triangle, the measure of an angle is 40°. Find the measure of other angles of the triangle in degrees.
In a right-angled triangle, the measure of an angle is 40°. Find the measure of other angles of the triangle in degrees.
- Area - simple
 Find the area of the triangle. So, the base is 7 2/3 mi. The height is 7 mi. What is the Area?
Find the area of the triangle. So, the base is 7 2/3 mi. The height is 7 mi. What is the Area? - The sides 7
 The sides of the triangle are 5.2, 4.6, and x. If the PERIMETER of the triangle is 11.2 feet, what is the length of the unknown side? (hint: draw a picture)
The sides of the triangle are 5.2, 4.6, and x. If the PERIMETER of the triangle is 11.2 feet, what is the length of the unknown side? (hint: draw a picture) - Two sides 2
 Two sides of a triangle are 12 and 15, and the perimeter is 40. Find the other side.
Two sides of a triangle are 12 and 15, and the perimeter is 40. Find the other side. - For triangle
 For triangle XYZ, ∠X = (6g + 14)° and the exterior angle to ∠X measures (5g + 45)°. Find the measure of ∠X and its exterior angle.
For triangle XYZ, ∠X = (6g + 14)° and the exterior angle to ∠X measures (5g + 45)°. Find the measure of ∠X and its exterior angle. - The perimeter 12
 The perimeter of an equilateral triangle is 41.46 inches. If the length of each side is (q - 5.7), what is the value of q?
The perimeter of an equilateral triangle is 41.46 inches. If the length of each side is (q - 5.7), what is the value of q?
- Three angles
 The three angles of a triangle are (3x-2)°, (4x+5)°, and (2x-3)°, then find the angles.
The three angles of a triangle are (3x-2)°, (4x+5)°, and (2x-3)°, then find the angles. - Perimeter - general
 Solve: the perimeter of a triangle is 4x+1.if two of it side are(x+2) and (x-1). Find the third side.
Solve: the perimeter of a triangle is 4x+1.if two of it side are(x+2) and (x-1). Find the third side. - The angles 4
 The angles of a triangle are divided into the ratio 126: 213: 312. If the three angles sum to 180°, find the size of each of the three angles.
The angles of a triangle are divided into the ratio 126: 213: 312. If the three angles sum to 180°, find the size of each of the three angles. - Angles sum 180
 In triangle ABC, the measure of ∠A is 30°, and the measure of ∠C is 90°. What is the measure of ∠B?
In triangle ABC, the measure of ∠A is 30°, and the measure of ∠C is 90°. What is the measure of ∠B? - A right
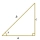 A right triangle has side lengths a=3, b=5, and c=4, as shown below. Use these lengths to find tan x, sin x, and cos x.
A right triangle has side lengths a=3, b=5, and c=4, as shown below. Use these lengths to find tan x, sin x, and cos x.
- Panting
 If the base of the triangle is 2 3/4 meters & and the altitude is 3 2/3 meters, then what is the cost of panting on both sides at ₹3 1/2 per sq.m.?
If the base of the triangle is 2 3/4 meters & and the altitude is 3 2/3 meters, then what is the cost of panting on both sides at ₹3 1/2 per sq.m.? - One side 3
 One side of a triangular banner is 1 1/2 times longer than the second side and 2cm shorter than the third side. The perimeter of the triangle is 98cm. How long is the shortest side?
One side of a triangular banner is 1 1/2 times longer than the second side and 2cm shorter than the third side. The perimeter of the triangle is 98cm. How long is the shortest side? - General right triangle
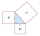 In a right triangle, if a =x+34 and b = x and c= 50, then solve for x. Side c is a hypotenuse. Then discuss the case when a or b is a hypotenuse.
In a right triangle, if a =x+34 and b = x and c= 50, then solve for x. Side c is a hypotenuse. Then discuss the case when a or b is a hypotenuse. - EE school boarding
 Three vectors, A, B, and C, are related as follows: A/C = 2 at 120 deg, A + B = -5 + j15, C = conjugate of B. Find C.
Three vectors, A, B, and C, are related as follows: A/C = 2 at 120 deg, A + B = -5 + j15, C = conjugate of B. Find C. - RST triangle
 Find out if it is possible to construct the given triangle and according to which theorem: RS = 2.5 cm ST = 7 cm TR = 4.5 cm
Find out if it is possible to construct the given triangle and according to which theorem: RS = 2.5 cm ST = 7 cm TR = 4.5 cm
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
