Circle practice problems - page 46 of 49
Number of problems found: 971
- Rectangular 13731
I have a rectangular trapezoid ZIMA (the right angle at the top of Z. ZIMA = winter in English) ZI-7cm, ZM-5cm, AM-3.5cm, and I have to write the procedure and perform a test in the design task - Circumference 7143
Peter drew a regular hexagon, the vertices of which lay on a circle 16 cm long. Then, for each vertex of this hexagon, he drew a circle centered on that vertex that ran through its two adjacent vertices. The unit was created as in the picture. Find the ci - Length of the arc
What is the arc length of a circle k (S, r=68mm), which belongs to a central angle of 78°? - Arc
The length of the circle is 18, and the arc length of the circle is 1. What is the magnitude of the angle of this arc?
- Hexagonal pyramid
The pyramid's base is a regular hexagon, which can be circumscribed in a circle with a radius of 1 meter. Calculate the volume of a pyramid 2.5 meters high. - Pavement
Calculate the length of the pavement that runs through a circular square with a diameter of 40 m if the distance of the pavement from the center is 15 m. - Equation of circle 2
Find the equation of a circle that touches the axis of y at a distance of 4 from the origin and cuts off an intercept of length 6 on the axis x. - Sprinkler 80801
A sprinkler is located in the park at a distance of 3m from the sidewalk. Water blasted up to a distance of max. 5m. What is the maximum length of the sidewalk it will cover? - The circle arc
Calculate the span of the arc, which is part of a circle with diameter d = 11 m and its height is 5 m.
- Field with vegetables
The field planted with vegetables has a rectangular isosceles triangle with a leg length of 24 m. At the triangle's vertices are rotating sprinklers with a range of 12 m. How much of the field sprinkler isn't irrigated? - Ground 8370
The arch has a radius of 3.3 m, a span of 3.25 m, and a height of 20 cm above the ground. What is the length of the arc to reach the ground? - Circle section
An equilateral triangle with side 33 is an inscribed circle section whose center is in one of the triangle's vertices, and the arc touches the opposite side. Calculate: a) the length of the arc b) the ratio between the circumference to the circle sector a - Subtended 83194
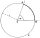A circle k with a center at point S and a radius of 6 cm is given. Calculate the size of the central angle subtended by a chord 10 cm long. - Goat and circles
What is the radius of a circle centered on the other circle, and is the intersection of the two circles equal to half the area of the first circle? This task is the mathematical expression of the role of agriculture. The farmer has circular land on which
- Circle sector
The circular sector with a central angle 160° has an area 452 cm². Calculate its radius r. - Tunnel boring
How much material did they dig when cutting the 400m long tunnel? The area of the circular segment, which is the cross-section of the tunnel, is 62m². - Situation 70644
How large is the area colored brown inside a square of side 6 cm if each of the four brown circular segments is from a circle with a radius of the length of the square's side? The length of the circular segments is equal to the length of the side of the s - Hexa pyramid
The base of the regular pyramid is a hexagon, which can be described as a circle with a radius of 2 m. Find the volume of the pyramid to be 2.5 m high. - Three segments
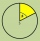The circle is divided into three segments. Segment A occupies 1/4 of the area. Segment B occupies 1/3 of the area. What part is occupied by section C? In what proportion are areas A: B: C?
A square with an area of 16 centimeters is inscribed circle k1 and described to circle k2. Calculate the area of the circular ring, which circles k1, and k2 form.Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
