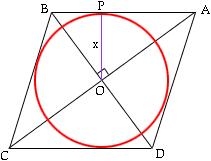
Circle in rhombus
An inscribed circle is in the rhombus. Contact points of touch divide the sides into parts of length 14 mm and 9 mm. Calculate the circle's area.
Correct answer:
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Chord 2
Point A has a distance of 13 cm from the circle's center with a radius r = 5 cm. Calculate the length of the chord connecting the points T1 and T2 of contact of tangents led from point A to the circle. - Square and circles
Square with sides 62 mm is circumscribed and inscribed with circles. Determine the radiuses of both circles. - Touch circle
Point A has a distance (A, k) = 10 cm from a circle k with radius r = 4 cm and center S. Calculate: a) the distance of point A from the point of contact T if the tangent to the circle is drawn from point A b) the distance of the contact point T from the l - Rhombus
It is given a rhombus with a side length of a = 20 cm. Touchpoints of the inscribed circle divided its sides into sections a1 = 13 cm and a2 = 7 cm. Calculate the radius r of the circle and the length of the diagonals of the rhombus.
- Circles 2
Calculate the area bounded by the circumscribed and inscribed circle in a triangle with sides 16 cm, 20 cm, and 15 cm. - Calculate 7214
Two tangents are drawn from point C to a circle with a radius of 76 mm. The distance between the two contact points is 14 mm. Calculate the distance of point C from the center of the circle. - Instructions: 56651
Divide the line segment AB into three equal parts. Instructions: Construct an equilateral triangle ABC and find its center (e.g., the described circles).
