Circumference 7143
Peter drew a regular hexagon, the vertices of which lay on a circle 16 cm long. Then, for each vertex of this hexagon, he drew a circle centered on that vertex that ran through its two adjacent vertices.
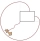
The unit was created as in the picture. Find the circumference of the marked flower.
The unit was created as in the picture. Find the circumference of the marked flower.
Correct answer:

Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Larger perimeter
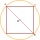 A square and a circle pass through two adjacent vertices of the square (endpoints of side a) and the center of the opposite side (c). Which of the plane shape has a larger perimeter?
A square and a circle pass through two adjacent vertices of the square (endpoints of side a) and the center of the opposite side (c). Which of the plane shape has a larger perimeter? - Combi-triangle
 Each square side is marked 10 different points outside the square's vertices. How many triangles can be constructed from this set of points, where each vertex of the triangle lies on the other side of the square?
Each square side is marked 10 different points outside the square's vertices. How many triangles can be constructed from this set of points, where each vertex of the triangle lies on the other side of the square? - Candy - MO
 Gretel deploys different numbers to the vertex of a regular octagon, from one to eight candy. Peter can then choose which three piles of candy to give Gretel others retain. The only requirement is that the three piles lie at the vertices of an isosceles t
Gretel deploys different numbers to the vertex of a regular octagon, from one to eight candy. Peter can then choose which three piles of candy to give Gretel others retain. The only requirement is that the three piles lie at the vertices of an isosceles t - Marlon
 Marlon drew a scale drawing of a summer camp. In real life, the sand volleyball court is 8 meters wide. It is 4 centimeters wide in the picture. What is the drawing's scale factor? Simplify your answer and write it as a ratio, using a colon.
Marlon drew a scale drawing of a summer camp. In real life, the sand volleyball court is 8 meters wide. It is 4 centimeters wide in the picture. What is the drawing's scale factor? Simplify your answer and write it as a ratio, using a colon.
- Grassland and goat
 An unfenced grassland is a right triangle ABC with AB = 4m, BC = 8m, and AC as hypotenuse. A goat is tied to a 5-m long rope with its stake at point O, which is 2m from side AB and 2m from the prolongation of side BC through corner B. Then: 1. How far is
An unfenced grassland is a right triangle ABC with AB = 4m, BC = 8m, and AC as hypotenuse. A goat is tied to a 5-m long rope with its stake at point O, which is 2m from side AB and 2m from the prolongation of side BC through corner B. Then: 1. How far is - Hexagon in circle
 Calculate the radius of a circle whose length is 10 cm greater than the circumference of a regular hexagon inscribed in this circle.
Calculate the radius of a circle whose length is 10 cm greater than the circumference of a regular hexagon inscribed in this circle. - Hexa pyramid
 The base of the regular pyramid is a hexagon, which can be described as a circle with a radius of 2 m. Find the volume of the pyramid to be 2.5 m high.
The base of the regular pyramid is a hexagon, which can be described as a circle with a radius of 2 m. Find the volume of the pyramid to be 2.5 m high.
