Quadrilateral and angles
In a quadrilateral, angle α is twice as large as angle β. Angle γ is 80% of angle α, and angle δ is 30° greater than angle α. Determine the angles of this quadrilateral.
Correct answer:
Tips for related online calculators
Our percentage calculator will help you quickly and easily solve a variety of common percentage-related problems.
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
You need to know the following knowledge to solve this word math problem:
- algebra
- equation
- system of equations
- arithmetic
- addition
- planimetrics
- quadrilateral
- basic functions
- percentages
Units of physical quantities:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Quadrilateral 7583
For the sizes of the interior angles of the quadrilateral ABCD, the following applies: the angle alpha is 26° greater than the angle beta, twice the angle Beta is 5° less than the angle gamma, and the angle gamma is 36° greater than the angle delta. Deter - Quadrilateral 81544
In the general quadrilateral ABCD, angle β is 9° greater than angle α, angle γ is 24° greater than angle α, and angle δ is 50° greater than angle β. Determine the sizes of individual angles. - Interior 39791
For the interior angles of a triangle, the angle β is twice as large, and the angle γ is three times larger than the angle α. Is this triangle right? - Quadrilateral 82395
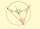The points ABC lie on the circle k(S, r) such that the angle at B is obtuse. How large must the angle at vertex B of quadrilateral SCBA be so that this angle is three times greater than the interior angle ASC of the same quadrilateral?
- Determine 82143
Determine the size of the interior angles in an isosceles triangle if you know that the angle opposite the base is 15° greater than the angles at the base. - Angle at the apex
In an isosceles triangle, the angle at the apex is 30° greater than the angle at the base. How big are the internal angles? - Angles of a triangle
In triangle ABC, the angle beta is 15° greater than the angle alpha. The remaining angle is 30° greater than the sum of the angles alpha and beta. Calculate the angles of a triangle.
