MO8-Z8-I-5 2017
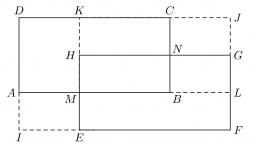
Identical rectangles ABCD and EFGH are positioned such that their sides are parallel to the same. The points I, J, K, L, M, and N are the intersections of the extended sides, as shown. The area of the BNHM rectangle is 12 cm², the rectangle MBCK area is 63 cm², and the rectangle MLGH area is 28 cm². Find the area of the IFJD rectangle.
Your answer:
Your answer:
You need to know the following knowledge to solve this word math problem:
planimetrybasic operations and conceptsUnits of physical quantitiesthemes, topicsGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Quadrangle ACEG
The figure shows two rectangles ABCD and DEFG, with |DE| = 3 cm, |AD| = 6 cm, |DG| = 5 cm, and |CD| = 10 cm. Calculate the area of quadrilateral ACEG. Figure description: the two rectangles share vertex D. Rectangle ABCD has sides twice as long as those o - Connecting lines
They are given a square ABCD. The points EFGH are the midpoints of its sides. What part of the area of the square ABCD is the area of the square created in its center by connecting the points AF, BG, CH, and DE? - Paper strip folding
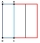A rectangular strip of paper measuring 4 cm x 13 cm is folded as shown. The two resulting rectangles have areas P and Q, where P = 2Q. Calculate the value of x. Note divide the side of 13 cm by x and 13-x. - Isosceles trapezoid 3
In isosceles trapezoid ABCD, calculate the unknown side length "a" and its area. Sides b = d = 50 cm, c = 20 cm, and the height = 48 cm. - Parallelogram
Calculate area of the parallelogram ABCD as shown if |AB| = 13 cm, |BC| = 99 cm and angle BAD = 100° - The rectangle 5
The rectangle OABC has one vertex at O, the center of a circle, and a second vertex, A, 2 cm from the edge of the circle, as shown. The vertex A is also 7 cm from C. The points B and C lie on the circumference of the circle. a. What is the radius? b. Find - Two 2D shapes
Decide which shapes have more area: (a) a square of 8 cm side, or (b) two rectangles with sides of 5 cm and 15 cm? Write the result as 1 or 2 (rectangles)
