Intersection 81017
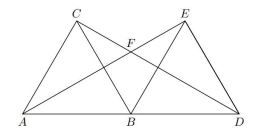
There are also two equilateral triangles ABC, and BDE, such that the size of the angle ABD is greater than 120° and less than 180° points C and E lie in the same half-plane defined by the line AD. The intersection of CD and AE is marked F. Determine the size of angle AFD.
Correct answer:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Themes, topics:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Internal angles
The ABCD is an isosceles trapezoid, which holds: |AB| = 2 |BC| = 2 |CD| = 2 |DA|: On the BC side is a K point such that |BK| = 2 |KC|, on its side CD is the point L such that |CL| = 2 |LD|, and on its side DA, the point M is such that | DM | = 2 |MA|. Det - Quadrilateral 82395
The points ABC lie on the circle k(S, r) such that the angle at B is obtuse. How large must the angle at vertex B of quadrilateral SCBA be so that this angle is three times greater than the interior angle ASC of the same quadrilateral? - MO - triangles
On the AB and AC sides of the ABC triangle lies successive points E and F, and on segment EF lie point D. The EF and BC lines are parallel. It is true this ratio FD:DE = AE:EB = 2:1. The area of the ABC triangle is 27 hectares, and line segments EF, AD, a - Distance 15203
In the plane, the points A, B, and C are given 3 cm apart, and they do not lie in the same straight line. Mark the set of all points whose distance from all three points is less than or equal to 2.5 cm.
- MO Z7–I–6 2021
In triangle ABC, point D lies on the AC side and point E on the BC side. The sizes of the angles ABD, BAE, CAE, and CBD are 30°, 60°, 20°, and 30°, respectively. Find the size of the AED angle. - Intersection 7247
On side AB of triangle ABC, points D and E are given such that |AD| = |DE| = |EB|. Points A and B are the midpoints of segments CF and CG. Line CD intersects line FB at point I, and line CE intersects line AG at point J. Prove that the intersection of lin - Bisectors
As shown, in △ ABC, ∠C = 90°, AD bisects ∠BAC, DE⊥AB to E, BE = 2, BC = 6. Find the perimeter of triangle △ BDE.
