Příklady na úhlopříčku lichoběžníku - poslední strana
Počet nalezených příkladů: 37
- Úhlopříčka
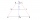Určete délku úhlopříčky BD v pravoúhlém lichoběžníku ABCD s pravým úhlem při vrcholu A, když /AD/=8,1 cm a úhel DBA je 42° - Rovnoramenný lichoběžník
Rovnoramenný lichoběžník ABCD o základnách délky |AB| = 6 cm, |CD| = 4 cm je diagonálami protínajícími se v bodě S rozdělen na 4 trojúhelníky. Jakou část plochy daného lichoběžníka zaujímají trojúhelníky ABS a CDS? - Lichoběžník IV
V lichoběžníku ABCD (AB||CD) platí |AB| = 15cm, |CD| = 7cm, |AC| = 12cm, AC je kolmé na BC. Jaký obsah má lichoběžník ABCD? - Čtyřúhelnících 37861
Které z následujících tvrzení o úhlech ve čtyřúhelnících je nepravdivé a. V pravoúhlém lichoběžníku je právě jeden vnitřní úhel tupý. b. Úhlopříčky kosočtverce svírají pravý úhel. c. Součet velikostí libovolných dvou vnitřních úhlů v rovnoběžníku je 180°.
- Lichoběžník 21
Je dán lichoběžníku ABCD s rovnoběžnými stranami AB a CD pro bod E strany AB plati, že úsečka DE dělí lichoběžník na dvě části se stejným obsahem. Spočítej délku úsečky AE. - Rovnoramenném 7537
Vypočtená délku ramen v rovnoramenném lichoběžníku. Výsledek zaokrouhlí na 2 desetinná místa. Úhlopříčka alfa se rovná 0,4 m a úhlopříčka beta se rovná 0,4 m. Strana AB má 120 cm a strana DC má 7,6 dm. - Lichoběžník MO-5-Z8 Lichoběžník ABCD je úsečkou CE rozdělen na trojúhelník a rovnoběžník, viz obrázek. Bod F je středem úsečky CE, přímka DF prochází středem úsečky BE a obsah trojúhelníku CDE je 3 cm². Určete obsah lichoběžníku ABCD.
- Lichoběžník
V rovnoramenného lichoběžníku KLMN je průsečík úhlopříček označen písmenem S. Vypočítejte obsah lichoběžníku, pokud /KS/: /SM/ = 2:1 a obsah trojúhelníku KSN je 14 cm². - Nepřístupných 69794
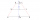Určete vzdálenost dvou nepřístupných míst P, Q, pokud vzdálenost dvou pozorovacích míst A, B je 2000m a znáte-li velikost úhlů QAB = 52°40'; PBA = 42°01'; PAB = 86°40' a QBA = 81°15'. Uvažovaná místa A, B, P, Q leží v jedné rovině.
- Lichoběžník 83
Lichoběžník ABCD je složen z pěti trojúhelníků. Body E, G dělí úsečku AB v poměru 2:4:3 (v tomto pořadí) na tři úsečky. Bod F je středem úsečky AD. Trojúhelník AEF je rovnoramenný a pravoúhlý. Trojúhelníky GBC a CDG jsou pravoúhlé. Obsah trojúhelníku AEF - MO Z8–I–6 2018
V lichoběžníku KLMN má základna KL velikost 40 cm a základna MN má velikost 16 cm. Bod P leží na úsečce KL tak, že úsečka NP rozděluje lichoběžník na dvě části se stejnými obsahy. Určete velikost úsečky KP. - V lichoběžníku 3
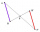V lichoběžníku ABCD jsou dány délky základen |AB| = 12 cm, |CD| = 8 cm. Bod S je průsečík úhlopříček, pro který platí |AS| = 6 cm. Vypočítej délku celé úhlopříčky AC. - Lichoběžník MO
Je dán pravouhlý lichoběžník ABCD s pravým uhlem u bodu B, |AC| = 12, |CD| = 8, uhlopříčky jsou na sebe kolmé. Vypočítejte obvod a obsah takéhoto lichobežníka. - Lichoběžník - úhlopříčky
Lichoběžník má délku úhlopříčky AC přeseknutu úhlopříčkou BD v poměru 2:1. Trojúhelník vytvořen body A, průnikem úhlopříček (S) a bodem D má obsah 164 cm². (Tomuto trojúhelníku také patří strana úhlopříčky AC a je 2x větší než její druhá část.) Jaký je ob
- V lichoběžníku
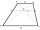V lichoběžníku ABCD jsou dány základny: AB = 12cm CD = 4 cm A úhlopříčky se protínají pod pravým úhlem. Jaký je obsah tohoto lichoběžníku ABCD? - MO Z9–I–2 - 2017
V lichoběžníku VODY je VO delší základnou a průsečík úhlopříček K dělí úsečku VD v poměru 3:2 . Obsah trojúhelníku KOV je 13,5 cm². Urči obsah celého lichoběžníku. - Čtyřboký hranol 6
Vypočítej povrch čtyřbokého hranolu ABCDA'B'C'D' s lichoběžníkovou podstavou ABCD. Výška hranolu je 12 cm; údaje o lichoběžníku ABCD: délka základny AB je 8 cm, délka základny CD je 3 cm, délka ramene BC je 4 cm a délka úhlopříčky AC je 7 cm. Napovíme: Na
Máš úkol, nad kterým si lámeš alespoň 10 minut hlavu? Pošli nám úkol a my Ti ji zkusíme vypočítat. Řešení příkladů z matematiky.
