Thaletova věta - příklady - strana 2 z 3
Pokyny: Vyřešte každý úkol pečlivě a ukažte své celé řešení. Pokud je to vhodné, proveďte zkoušku správnosti řešení.Počet nalezených příkladů: 45
- V lichoběžníku
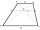V lichoběžníku ABCD jsou dány základny: AB = 12cm CD = 4 cm A úhlopříčky se protínají pod pravým úhlem. Jaký je obsah tohoto lichoběžníku ABCD? - Kružnice opsaná
Poloměr kružnice opsané pravoúhlému trojúhelníku s odvěsnou dlouhou 6 cm, je 5 cm. Vypočítej obvod tohoto trojúhelníku. - Rovnoramenný 7566
Do kruhu s r=8cm byl vepsán pravoúhlý rovnoramenný trojúhelník. Zjisti jeho S. Kolik % zabírá trojúhelník z plochy kruhu? - Amfiteátr 7562
Amfiteátr má tvar půlkruhu. Pódium je průměr půlkruhu. Diváci K, L, M, N, O sedí po obvodu. Kdo vidí pódium pod největším úhlem?
- Sestrojte 6770
Je dána kružnice k(S;2,5cm) a bod L pokud |SL|=4cm. Sestrojte tečnu ke kružnici, která prochází bodem L. - Dvě výšky a strana
Sestrojte trojúhelník ABC, když je daná strana c = 7 cm, vyška na a: va = 5 cm a vyška na b: vb = 4 cm. - Stejný obsah
Je dán trojúhelník. Sestroj čtverec se stejným obsahem. - Pravouhlý trojuholník
Trojúhelník má přeponu 55 a výšku na přeponou 33. Jaká je plocha trojúhelníku? - Thalet
Jsou dány dva body K a L, KL= 4 cm. Sestroj přímku p, která prochází bodem K a od bodu L má vzdálenost 4 cm.
- Tečna
Je dána kružnice k se středem S a poloměrem 3,5cm. Vzdálenost přímky p od středu je 6 cm. Sestrojte tečnu kružnice n, která je kolmá na přímku p - Úplná konstrukce
Sestrojte trojúhelník ABC, přepona c = 7 cm, úhel ABC=30 stupňů. /Použijte Thaletovu kružnici/. Změřte a napište délku odvěsen. - Sestroj OP
Je dána kružnice k (S; 2,5 cm) a vnější přímka p. Sestroj tečnu t této kružnice, která s přímkou p svírá úhel 60°. Kolik řešení má úkol? - Sestroj
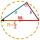Sestroj trojúhelník ABC, a = 7 cm, b = 9 cm, pravý úhel u vrcholu C, sestroj osy všech tří stran. Odmerajte a zapíšte délku strany c. - Vrcholy
Sestrojte vrcholy C všech trojúhelníků ABC, je-li dána strana AB, výška vb na stranu b a délka těžnice tc na stranu c. Sestrojte všechna řešení. Vrcholy označte C1, C2,. ..
- Sestroj troj-ssu
Sestroj trojúhelník ABC: |AB|=5cm, v_a=3cm, CAB=50°. Má se vytvořit rozbor, popis a konstrukce. - Vepsán trojúhelník
Do kružnice je vepsán trojúhelník tak, že jeho vrcholy dělí kružnici na 3 oblouky. Délky oblouků jsou v poměru 2:3:7. Urči vnitřní úhly trojúhelníka. - Trojúhelník
Narysuj pravoúhlý trojúhelník ABC, ve kterém platí: |AB| = 5 cm, |BC| = 3 cm, |AC| = 4 cm. Zostroj Thaletovu kružnici nad přeponou trojúhelníku ABC. - Tětiva
Strana trojúhelníku vepsaného do kružnice je tětivou procházející jejím středem. Jakou velikost mají vnitřní úhly trojúhelníku, pokud jeden z nich má 40°? - Most
Přes jezero, které má tvar kruhu, prochází most přesně přes střed jezera. Na třech různých místech na břehu jezera se nacházejí tři rybáři A, B, C. Který z rybářů vidí celý most pod největším úhlem?
V půlkruhu se středem S a průměrem AB je sestrojen rovnostranný trojúhelník SBC. Jaká je velikost úhlu ∠ SAC?Máš úkol, nad kterým si lámeš alespoň 10 minut hlavu? Pošli nám úkol a my Ti ji zkusíme vypočítat. Řešení příkladů z matematiky.
