Sinus - příklady - strana 3 z 16
Počet nalezených příkladů: 317
- Zaokrouhlete 72864
Muž, který se toulá pouští, ujede 3,8 míle ve směru S 44° W západní délky. Potom se otočí a ujede 2,2 míle ve směru severní N 55° W západní délky. Jak daleko je v té době od svého výchozího bodu? (Vaši odpověď zaokrouhlete na dvě desetinná místa.) - Kosočtverec 72824
Kosočtverec má délku strany 10 cm. Najděte úhly v každém rohu kosočtverce, pokud kratší ze dvou úhlopříček měří 7 cm. Uveďte své odpovědi na nejbližší stupeň a uveďte jasné geometrické úvahy v každé fázi vašeho řešení. - Horizontální 72204
Turista plánuje túru na jednu stranu hory a dolů na druhé straně vrcholu hory, přičemž každá strana hory je tvořena přímkou. Úhel elevace v počátečním bodě je 42,4 stupně a úhel elevace na konci je 48,3 stupně_ Horizontální vzdálenost mezi počátečním a ko - Pozorovatelně 71934
Letadlo letící směrem k pozorovatelně, z ní bylo zaměřeno v přímé vzdálenosti 5300 m pod výškovým úhlem 28º a po 9 sekundách v přímé vzdálenosti 2400 m pod výškovým úhlem 50º. Vypočítejte vzdálenost, kterou v tomto časovém intervalu letadlo prolétlo, jeho
- Vzdálenost 71874
Hlídka měla určený pochodový úhel 13°. Po ujetí 9 km se úhel změnil na 62°. Tímto směrem šla hlídka 10 km. zjistí vzdálenost od místa, ze kterého hlídka vyšla. - Hloubkový úhel
Maják vidí loď pod hloubkovým úhlem 25°. Pozorovatel z majáku je ve výšce 82 m nad mořem. Jak daleko je loď od vrchu majáku? - Vypočítej 70744
Vypočítej objem a povrch rotačního kužele, pokud jeho výška je 10 cm a strana má od roviny podstavy odchylku 30°. - F(x)=(e^x)/((e^x)+1) 70464
Funkce: f(x)=xtanx f(x)=(e^x)/((e^x)+1) Najít; i) vertikální a horizontální asymptoty iii) intervaly poklesu a růstu iii) Místní maxima a místní minima iv) interval konkávnosti a inflexe. A načrtněte graf. - Kosočtverce 70334
Jaká je výška kosočtverce se stranou 6 cm dlouhou, pokud úhel, který svírají vedlejší strany je 78 stupňů a 10'?
- Nepřístupných 69794
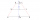Určete vzdálenost dvou nepřístupných míst P, Q, pokud vzdálenost dvou pozorovacích míst A, B je 2000m a znáte-li velikost úhlů QAB = 52°40'; PBA = 42°01'; PAB = 86°40' a QBA = 81°15'. Uvažovaná místa A, B, P, Q leží v jedné rovině. - Střídavého 69064
Popište, jak se mění okamžitá hodnota výkonu v obvodu střídavého proudu během jedné periody. - Adam (A)
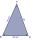Adam (A) stojí na jednom břehu řeky, Bedřich (B) stojí na druhém. Aby mohla být stanovena jejich vzdálenost, byla na jednom břehu řeky změřena základna AC o délce 136 m a úhly CAB s velikostí 70°21´ a ACB s velikostí 43°44´. Jaká je vzdálenost Adama a Bed - Síla R
Síla R = 12 N se má rozdělit na dvě složky F1, F2, jejich směry svírají se směrem síly R úhly α = 30°, β = 45°. Jaké jsou složky F1, F2? - Budova 3
Budova vysoká 15 m je vzdálená od břehu řeky 30 m. Ze střechy této budovy je vidět šířku řeky pod úhlem 15°. Jak je řeka široká?
- Rovnoběžníku 65334
V rovnoběžníku je součet délek stran a+b = 234. Úhel sevřený stranami a a b je 60°. Délka úhlopříčky proti danému úhlu 60° je u=162. Vypočítejte strany rovnoběžníku, jeho obvod a obsah. - Vypočítejte 64864
Vypočítejte délku stínu, který vrhá metrová tyč v pravé poledne, nacházející se na rovině poledníku a odchýlená od vodorovné roviny k severu o úhel velikosti 70°, pokud Slunce kulminuje pod úhlem 41°03'. - Trojúhelníku 64704
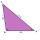V trojúhelníku ABC určí velikost stran a a b a velikosti vnitřních úhlů β a γ, je-li dáno c = 1,86 m, těžnice na stranu c je 2,12 m a úhel alfa je 40°12'. - Těžnice a střed
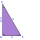Bod S je střed přepony AB pravoúhlého trojúhelníku ABC. Vypočítejte obsah trojúhelníku ABC, je-li těžnice na přeponu dlouhá 0,2 dm a platí-li |∢ACS| = 30°. - Trojúhelníku 64514
V trojúhelníku ABC platí a: b = 3:2 a α: β = 2:1. Vypočítejte poměr a: c.
Cíl C pozorovali ze dvou dělostřeleckých pozorovatelen A, B, které jsou od sebe vzdáleny 975m, přitom velikost úhlu BAC je 63°, velikost ABC je 48°. Vypočítejte vzdálenost bodů A a C.Máš úkol, nad kterým si lámeš alespoň 10 minut hlavu? Pošli nám úkol a my Ti ji zkusíme vypočítat. Řešení příkladů z matematiky.
